Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M, N, P lần lượt là trung điểm của EF, EG, HG
∆AEF vuông tại A có AM là trung tuyến nên AM = 1/2EF
∆HCG vuông tại C có CP là trung tuyến nên CP = 1/2GH
∆EFG có MN là đường trung bình nên MN = 1/2FG
∆EGH có NP là đường trung bình nên NP = 1/2EH
Chu vi tứ giác EFGH bằng EF + FG + GH + HE = 2(AM + MN + NP + PC) ≥ 2AC
Dấu "=" xảy ra khi A, M, N, P, C thẳng hàng theo thứ tự đó
<=> FG // AC // EH, EF // BD // HG <=> Tứ giác EFGH là hình bình hành
Cách xác định điểm: Lấy điểm F trên AB sao cho EF // BD, sau đó lần lượt lấy các điểm H, G trên CD, BC sao cho EH // AC // FG

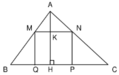
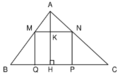
Vì ∆ ABC đồng dạng với ∆ AMN nên:
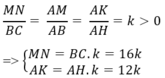
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
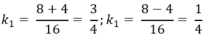
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
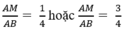

Vì ∆ ABC đồng dạng với ∆ AMN nên:
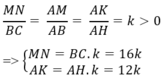
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
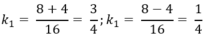
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
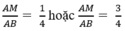

Vì E thuộc cạnh AB nên EB < AB hay 2x < y
Ta có: AE = AB – EB = y – 2x (cm)
AG = AD + DG = y + (3/2) EB = y + (3/2) .2x = y + 3x (cm)
Diện tích hình chữ nhật bằng diện tích hình vuông nên ta có phương trình:
(y – 2x)(y + 3x) = y 2
Theo định lí Pitago, ta có: F C 2 = E B 2 + D G 2
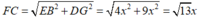
Chu vi ngũ giác ABCFG:
PABCFG = AB + BC + CF + FG + GA
= AB + BC + CF + FG + GD + DA
= y + y + x 13 + y – 2x + 3x + y = x(1 + 13 ) + 4y
Vì chu vi ngũ giác ABCFG bằng 100 + 4 13 (cm) nên ta có phương trình:
x(1 + 13 ) + 4y = 100 + 4 13
Ta có hệ phương trình:
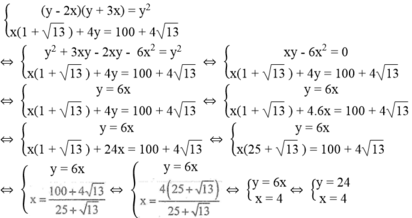
Giá trị của x và y thỏa điều kiện bài toán.
Vậy x = 4 (cm), y = 24 (cm).