Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

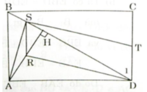
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)
⇒ ΔAHD ∼ ΔDCB (g.g)
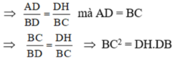
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB
⇒ ∠HSR = ∠HBA (đồng vị)
Mà ∠HBA = ∠D1
⇒ HSR = ∠D1
Do đó ΔSHR ∼ ΔDCB (g.g)
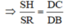
![]()
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2
mà AB = CD và AB // CD (gt)
⇒ SR // DT và SR = DT
Do đó Tứ giác DRST là hình bình hành
d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o

a: Xét ΔABD vuông tại A có AH là đường cao
nên \(AD^2=DH\cdot DB=BC^2\)
c: Xét ΔHAB có
R là trung điểm của HA
S là trung điểm của HB
Do đó: RS là đường trung bình
=>RS//AB và RS=AB/2
=>RS//DT và RS=DT
=>RSTD là hình bình hành

Giải chi tiết:
a) Xét tam giác AHD có:
M là trung điểm của AH (gt)
N là trung điểm của DH (gt)
Do đó MN là đường trung bình của tam giác AHD
Suy ra MN//AD (tính chất) (đpcm)
b) Ta có MN//AD, mà AD//BC (2 cạnh đối hình chữ nhật) nên MN//BC hay MN//BI Vì MN = 1212AD (tính chất đường trung bình của tam giác) và BI = IC = 1212BC (do gt), mà AD = BC (2 cạnh đối hình chữ nhật) MN = BI BC hay MN//BI Xét tứ giác BMNI có MN//BI, MN = BI (c/m trên) Suy ra tứ giác BMNI là hình bình hành (đpcm)
c) Ta có MN//AD và AD⊥⊥AB nên MN⊥⊥AB
Tam giác ABN có 2 đường cao là AH và NM cắt nhau tại M nên M là trực tâm của tam giác ABN. Suy ra BM⊥⊥AN.
Mà BM//IN nên AN⊥⊥NI hay ΔANIΔANI vuông tại N (đpcm)
# M̤̮èO̤̮×͜×L̤̮ườI̤̮◇

a) Xét tam giác AHD, có:
* M,N lần lượt là trung điểm của AH, DH (gt)
=> MN là đường trung bình của tam giác AHD
=> MN // AD (t/c) (đpcm)
b) Ta có: BC // AD (ABCD là hình chữ nhật)
=> MN // BI (I thuộc BC) (1)
Ta lại có: I là trung điểm BC (gt)
=> BI = AD : 2 (BC = AD)
Mà MN = AD :2 (MN là đường trung bình tam giác AHD)
=> BI = MN (2)
Từ (1), (2) => MBIN là hình bình hành (đpcm)
c) Xét tam giác AHN vuông tại N có:
* NM là trung tuyến (M là trung điểm AH)
=> NM = MA = MH (hệ quả)
=> tam giác AMN là tam giác cân tại M
Mà MB là đường nối từ đỉnh của tam giác cân AMN
=> MB là đường cao của tam giác AMN
=> góc AMB = 90 độ
=> AD vuông góc với MB
Mà MB // ID (MDIB là hình bình hành)
=> ID vuông góc với AD
=> góc ANI = 90 độ
P/S: Không chắc câu c) cho lắm.

câu 2d
Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)
⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA
Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA
Vậy ∠AST = 90o
...
Chúc bạn học tốt
câu 1d
+ ΔACI có BF//CI→ FC/FA=OI/AO
IΔCOI có AJ//CI (//BF)→ CI/AJ=OI/AO
→FC/FA=CI/AJ

a: Xét ΔAHD có
M là trung điểm của HA
N là trung điểm của HD
Do đó: MN là đường trung bình của ΔAHD
Suy ra: MN//AD
