Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé. mình mới nghĩ ra câu a vs c
a) Xét tứ giác AEBN có : EM=EN ( E đối xứng N qua M )
AM=MB ( M là TĐ' của AB )
=> Tg AEBN là hình bình hành ( Tg có 2 đường chéo cắt nhau tại trung điểm của mỗi đường là hbh )
mà EN vuông góc với AB ( E đối xứng N qua M )
=> hbh AEBN là hình thoi ( hbh có 2 đường chéo vuông ^ vs nhau là hình thoi )
c) Ta có AB=3BC (gt)
=> 6=3. BC=> BC=2cm
SABCD= a.b = 6.2 = 12 (cm2)
Mặt khác: AEBN là hình thoi (cmt)
=>EM=MN=2cm
SAEB = a.h:2 = 6.2:2 = 3 (cm2 )
Vậy SAEBCD= SABCD+SAEB=12+2=14 (cm2)

a: Xét tứ giác AHBD có
M là trung điểm chung của AB và HD
góc AHB=90 độ
=>AHBD là hình chữ nhật
b: \(AH=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(S_{AHBD}=6\cdot8=48\left(cm^2\right)\)
c: Xét ΔABC có AM/AB=AI/AC
nênMI//BC
Xét ΔBAC có CN/CB=CI/CA
nên NI//AB và NI/AB=CN/CB=1/2
=>NI=HM
Xét tứ giác MINH có
MI//HN
MH=IN
Do đó: MINH là hình thang cân

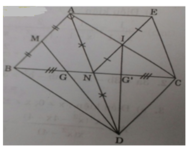
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)