Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

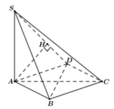
Xác định được ![]()
Khi đó ta tính được ![]()
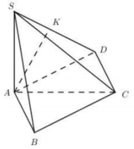
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật
=> AB//CD nên
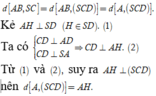
Xét tam giác vuông SAD có 
Chọn C.

Đáp án C
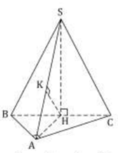

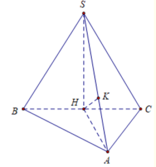
Từ (1), (2) => HK là đoạn vuông góc chung của SA và BC

Tam giác SHA vuông tại A có đường cao HK nên 1 HK 2 = 1 SH 2 + 1 AH 2 = 4 3 a 2 + 4 a 2 = 16 3 a 2 .
⇒ HK = 3 a 4 .
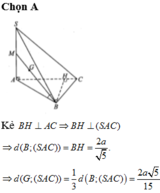

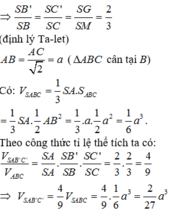

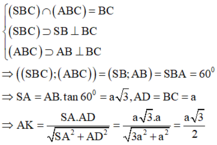



Phương pháp:
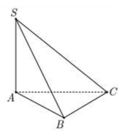
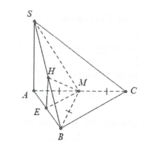
+) Gọi M, N, P, Q lần lượt là trung điểm của AB, SC, BC, AC. Chứng minh ∠ S A ; B C = ∠ N Q ; M Q
+) Áp dụng định lí cosin trong tam giác MNQ.
Cách giải:
Áp dụng định lý cosin trong tam giác MNQ:
Chú ý: Góc giữa hai đường thẳng là góc nhọn nên cosin của góc giữa hai đường thẳng là giá trị dương.