Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Gọi M là trung điểm AB \(\Rightarrow AB\perp OM\Rightarrow AB\perp\left(SOM\right)\)
\(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy hay \(\widehat{SMO}=60^0\)
\(SO=OM.tan\widehat{SMO}=\dfrac{a}{2}.tan60^0=\dfrac{a\sqrt{3}}{2}\)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.a^2=\dfrac{a^3\sqrt{3}}{6}\)

Chọn A.
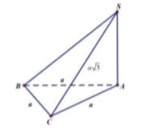
Ta có:
( S A B ) ⊥ ( A B C ) ( S A C ) ⊥ ( A B C ) ( S A B ) ∩ ( S A C ) = S A ⇒ S A ⊥ ( A B C )
S A B C = a 2 3 4 , S A = a 2
Vậy thể tích khối chóp V A B C = a 3 6 12

Đáp án là A
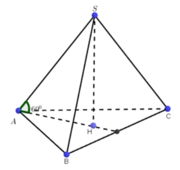
Ta có:
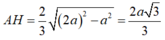
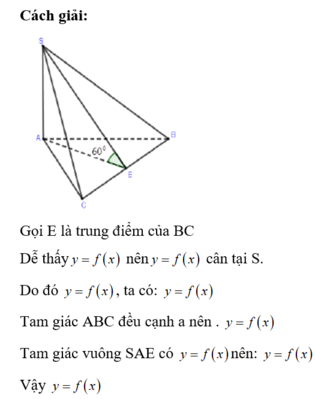
Theo giả thiết cạnh bên tạo đáy góc 60 0 suy ra góc SAH= 60 0
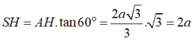
là tam giác đều cạnh 2a nên diện tích là
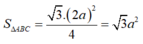
Thể tích khối chóp S.ABC là
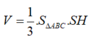
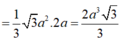

Chọn B
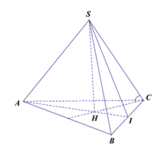
Gọi H là trọng tâm tam giác ABC, khi đó
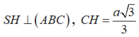
Góc giữa cạnh bên và mặt đáy là góc
![]()

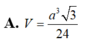
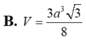
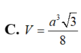
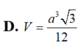

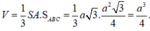
Đáp án A