Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
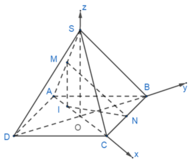
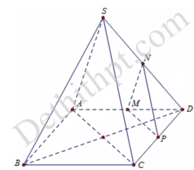
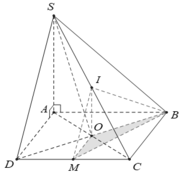
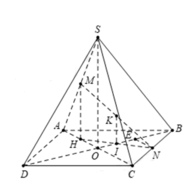
Gọi I là hình chiếu của M lên (ABCD), suy ra I là trung điểm của AO.
Khi đó
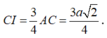
Xét tam giác CNI có
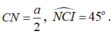
Áp dụng định lý cosin ta có:
![]()

Xét tam giác MIN vuông tại I nên
![]()
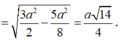
Mà MI//SO
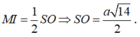
Chọn hệ trục tọa độ như hình vẽ. Ta có:
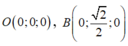
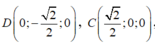
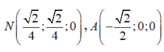
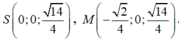
Khi đó
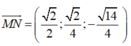
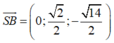
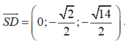
Vectơ pháp tuyến mặt phẳng (SBD)
![]()
Suy ra
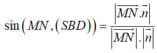
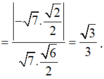

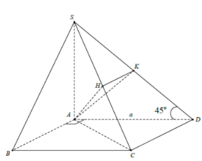
❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)

Gọi I là chân đường vuông góc kẻ từ H lên SC
Vì MD ⊥ (SCN), MD ∩ (SCN) = H nên
d(MD, SC) = d(H, SC) = HI = HC.sin60
°
= 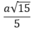
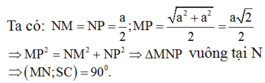
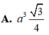
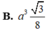

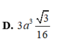

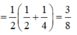



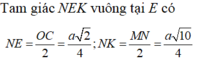

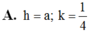
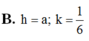
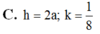
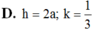

Đáp án C
MN là đường trung bình của tam giác DAS nên MN//SA
Gọi O là tâm của hình vuông ABCD, vì SA=SC=SB=SD nên SO ⊥ (ABCD)