Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
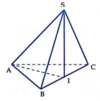
Gọi I là hình chiếu của điểm S trên mặt phẳng (ABC). Do SA = SB = SC nên IA = IB = IC => I là tâm đường tròn ngoại tiếp ∆ ABC . Mà ∆ ABC vuông cân tại A nên I là trung điểm của BC và IA = IB = IC = BC/2 = a 2 2
Ta có IA là hình chiếu của SA trên mặt phẳng (ABC) nên
![]()
Do ∆ SIA vuông tại I nên vuông cân tại I, khi đó :
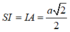
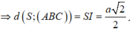

Chọn A
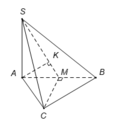
Xác định được
![]()
![]()
Do M là trung điểm của cạnh AB nên
![]()
![]()
![]()
Tam giác vuông SAM có
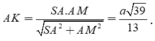
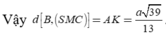

Chọn C
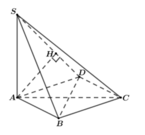
Xác định được
![]()
Khi đó ta tính được
![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật => AB//(SCD) nên
![]()
![]()
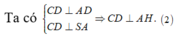
Từ (1) và (2) suy ra
![]()
Xét tam giác vuông SAD có
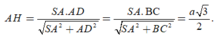
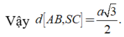

Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
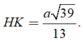

a: BC vuông góc AM
BC vuông góc SA
=>BC vuông góc (SAM)
b: BC vuông góc (SAM)
=>BC vuông góc SM
=>(SM;(ABC))=90 độ

Đáp án D.
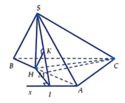
Kẻ Ax//BC, HI ⊥ Ax; HK ⊥ SI.
Gọi M là trung điểm của AB
![]()
![]()
Ta có AI ⊥ (SHI)=> AI ⊥ HK=> HK ⊥ (SAI)=>d(H,(Sax)) = HK
Góc giữa SC và (ABC) là góc S C H ^ = 60 0
Ta có:
![]()
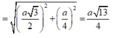
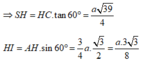
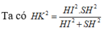
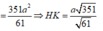
![]()
![]()

a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)

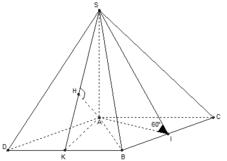
+) Hình chiếu vuông góc của SI trên mặt phẳng (ABC) là AI nên góc giữa SI và mặt phẳng (ABC) là:
(vì tam giác SIA vuông tại A nên góc SIA nhọn) ⇒ 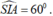
+) Xét tam giác SIA vuông tại A, 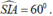
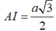 nên:
nên:
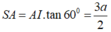
+) Dựng hình bình hành ACBD, tam giác ABC đều nên tam giác ABD đều.
+) Ta có:
AC // BD; BD ⊂ (SBD) nên AC // (SBD).
mà SB ⊂ (SBD) nên d(AC, SB) = d(A, (SBD)).
- Gọi K là trung điểm đoạn BD, tam giác ABD đều suy ra AK ⊥ BD và 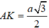 mà BD ⊥ SA nên BD ⊥ (SAK).
mà BD ⊥ SA nên BD ⊥ (SAK).
- Dựng AH ⊥ SK; H ∈ SK.
- Lại có AH ⊥ BD suy ra AH ⊥ (SBD).
- Vậy d(A, (SBD)) = AH.
- Xét tam giác SAK vuông tại vuông tại A, đường cao AH ta có:
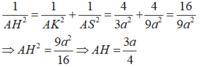
- Vậy d(AC, SB) = d(A, (SBD))
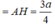
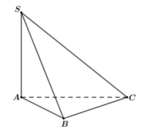

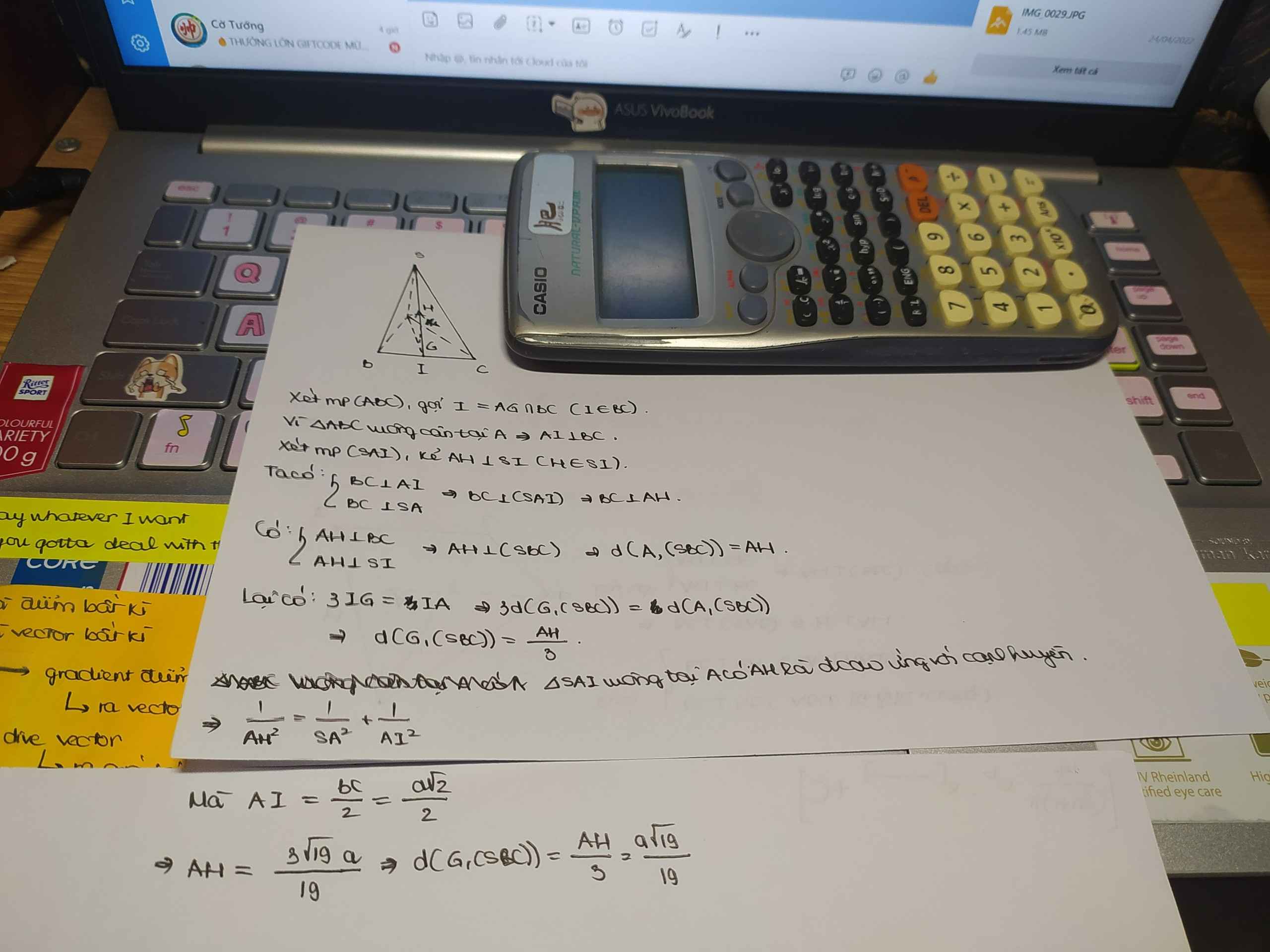
Đáp án B
Hình chiếu của S xuống đáy ABC là tâm của đáy tức là M với M là trung điểm của BC.
Ta có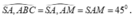
Vì ABC là tam giác vuông cân nên H cũng là trung điểm của vì thế
Ta có: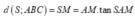
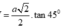 =
a
2
2
=
a
2
2