

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a. Do M, N là trung điểm AD, BC \(\Rightarrow MN||AB||CD\)
Gọi Q là trung điểm SA
\(\Rightarrow PQ\) là đường trung bình tam giác SAB
\(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow Q\in\left(MNP\right)\)
\(\Rightarrow Q=SA\cap\left(MNP\right)\)
b. Do Q là trung điểm SA, M là trung điểm AD
\(\Rightarrow MQ\) là đường trung bình tam giác SAD \(\Rightarrow MQ||SD\)
Mà \(MQ\in\left(MNP\right)\Rightarrow SD||\left(MNP\right)\)
Tương tự ta có \(NP||SC\) (đường trung bình) (1)
\(\left\{{}\begin{matrix}AM=NC=\dfrac{1}{2}AD\\AM||NC\end{matrix}\right.\) \(\Rightarrow AN||CM\) (2)
(1);(2) \(\Rightarrow\left(SMC\right)||\left(ANP\right)\)
c. Đề bài không tồn tại điểm L

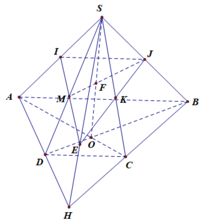
Kéo dài AD và BC cắt nhau tại E
\(\Rightarrow SE=\left(SAD\right)\cap\left(SBC\right)\)
Trong mp (SBC), nối MN kéo dài cắt SE tại F
Trong mp (SAD), nối AF cắt SD tại I
\(\Rightarrow I=SD\cap\left(AMN\right)\)
Tứ giác AINM chính là thiết diện của (AMN) và chóp
MN là đường trung bình tam giác SCD \(\Rightarrow F\) là trung điểm SE
Mặt khác CD song song và bằng 1/2 AB \(\Rightarrow\) CD là đường trung bình tam giác ABE hay D là trung điểm AE
\(\Rightarrow\) I là trọng tâm tam giác SAE
\(\Rightarrow\dfrac{SI}{SD}=\dfrac{2}{3}\)

1.
Gọi \(O=AC\cap BD\)
\(AM\in\left(SAC\right)\)
Mà \(\left(SAC\right)\cap\left(SBD\right)=SO\)
\(\Rightarrow J=AM\cap SO\)
Qua M kẻ \(d//AB\Rightarrow N=d\cap SD\)

Áp dụng định lý Talet trong tam giác KAD:
\(\dfrac{KB}{KA}=\dfrac{KC}{KD}=\dfrac{BC}{AD}=\dfrac{1}{2}\)
\(\Rightarrow B,C\) lần lượt là trung điểm AK và DK
Mà E, F là trung điểm SA, SD
\(\Rightarrow\) M, N lần lượt là trọng tâm các tam giác SAK và SDK
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{2}{3}\) ; \(\dfrac{SN}{SC}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{SM}{SB}=\dfrac{SN}{SC}=\dfrac{2}{3}\) (Talet)
\(\Rightarrow MN=\dfrac{2}{3}BC=\dfrac{2}{3}.\dfrac{1}{2}AD=\dfrac{1}{3}AD\)
Lại có EF là đường trung bình tam giác SAD \(\Rightarrow EF=\dfrac{1}{2}AD\)
\(\Rightarrow\dfrac{S_{KMN}}{S_{KEF}}=\dfrac{MN}{EF}=\dfrac{\dfrac{1}{3}AD}{\dfrac{1}{2}AD}=\dfrac{2}{3}\)

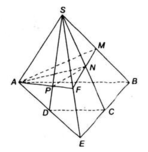
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
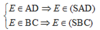
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.