Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

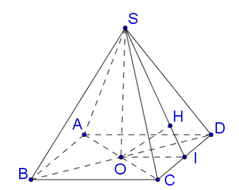
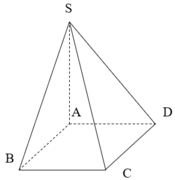
\(\left\{{}\begin{matrix}BD\perp SO\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ O kẻ \(OH\perp SA\) (H thuộc SA)
Do \(OH\in\left(SAC\right)\Rightarrow BD\perp OH\)
\(\Rightarrow OH\) là đường vuông góc chung BD và SA hay \(OH=d\left(BD;SA\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\) ; \(SO=\sqrt{SA^2-AO^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow\Delta SAO\) vuông cân tại O
\(\Rightarrow OH=\dfrac{1}{2}SA=\dfrac{a}{2}\)

a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=1/2
=>góc SDA=27 độ

a: CD vuông góc AD
CD vuông góc SA
=>CD vuông góc (SAD)
b: (SD;(ABCD))=(DS;DA)=góc SDA
tan SDA=SA/AD=1/2
=>góc SDA=27 độ
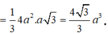
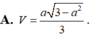
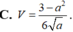
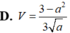
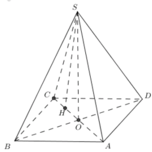
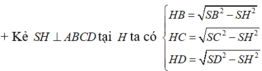
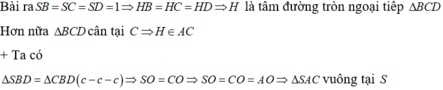
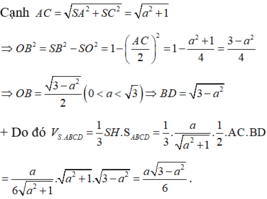
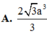
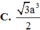
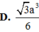
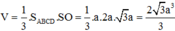
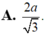
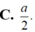
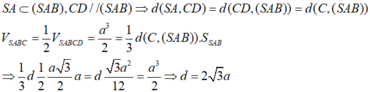
Đáp án D.