Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

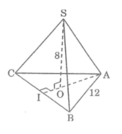
Kẻ AO kéo dài cắt BC tại I
Ta có: AI ⊥ BC (tính chất tam giác đều)
BI = IC = 1/2 BC
Áp dụng định lí pi-ta-go vào tam giác vuông AIB,ta có:
A B 2 = B I 2 + A I 2
Suy ra: A I 2 = A B 2 - B I 2 = 12 2 - 6 2 =108
AI = 108 cm
Vì tam giác ABC đều nên O là trọng tâm của tam giác ABC
Ta có: OI = 1/3.AI = 1/3. 108 cm
Áp dụng định lí pi-ta-go vào tam giác vuông SOI ta có:
S I 2 = S O 2 + O I 2 = 8 + 1/9 .108 = 76
SI = 76 cm
Vậy S x q = Pd= [(12.3):2]. 76 =18 76 cm

a:ΔSBC cân tại S có SM là trung tuyến
nên SM vuông góc BC
BC=6cm
=>BM=CM=3cm
SM=căn 5^2-3^2=4cm
Sxq=5*3/2*4=5*3*2=30cm2
Stp=30+5^2*căn 3/2=(60+25căn 3)/2cm2
b: BC vuông góc SM
BC vuông góc AM
=>BC vuông góc (SAM)

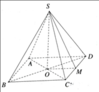

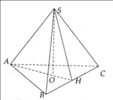


a) Chân đường cao H của hình chóp S.ABC trùng với trọng tâm của tam giác ABC.
Gọi M là trung điểm của BC
Tam giác ABC có
b) Tam giác SAM cân ở M nên
Diện tích xung quanh của hình chóp:
c) Diện tích toàn phần của hình chóp:
d) Thể tích của hình chóp