Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
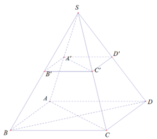
A’B’ // AB ( A’, B’ lần lượt là trung điểm SA, SB)
B’C’ // BC (B’, C’ lần lượt là trung điểm SB, SC)
Mà A’B’ và B’C’ cắt nhau; AB và BC cắt nhau.
⇒ (A’B’C’D’) // (ABCD)
⇒ (A’C’D’) // (ABC)

Đáp án A
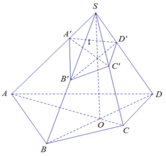
Xác định mặt phẳng (A’B’C’D’)
Lấy A’, B’, C’ lần lượt nằm trên SA, SB, SC
⇒ D’ thuộc mặt phẳng (A’B’C’)
Gọi O = AC ∩ BD
Trong (SAC) có: I = SO ∩ A ' C '
Trong (SBD) có: B ' I ∩ SD = D '
Từ cách dựng mặt phẳng (A’B’C’D’) ta thấy: SO, A’C’, B’D’ đồng quy tại I

Đáp án B
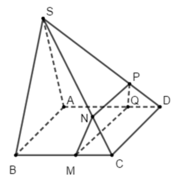
Ta có: MN // BS ⇒ C M C B = C N C S
MQ // CD // AB (do ABCD là hình bình hành nên AB //CD) ⇒ C M C B = D Q D A
NP // CD ⇒ C N C S = D P D S
Do đó: D P D S = D Q D A PQ // SA (Định lý Ta - lét trong tam giác SAD)
Lại có MN // BS và SB ∩ SA = S
Do đó MN không thể song song với PQ
Xét tứ giác MNPQ có NP // MQ (//CD)
Do đó MNPQ là hình thang.
Vậy khẳng địn (1) và (3) đúng.
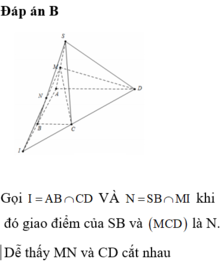
Đáp án B
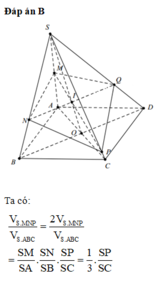

không nói được lời tử tế thì phiền đi chỗ khác=))