Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tớ biết làm nè
.
.
.
.
.
.
.
.
.
.
.
Biết làm cl í, tin người vcl:))

Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)

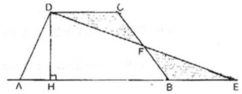
Gọi F là trung điểm của cạnh bên BC. Cắt hình thang theo đường DF đưa ghép về như hình vẽ bên, điểm C trung với điểm B, D trùng với E.
Vì AB // CD ⇒ ∠ (ABC) = 180 0 ⇒ A, B, E thẳng hàng
∠ (ABF) + ∠ (DFC) = 180 0
⇒ D, F, E thẳng hàng
△ DFC = △ EFB (g.c.g)
S D F C = S E F B
Suy ra: S A B C D = S A D E
△ DFC = △ EFB⇒ DC = BE
AE = AB + BE = AB + DC
S A D E = 1/2 DH. AE = 1/2 DH. (AB + CD)
Vậy : S A B C D = 1/2 DH. (AB + CD)

a) \(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{10+6}{2}.5=40\left(cm^2\right)\)
b) Xem hình vẽ
Tam giác vuông EAD có: \(AE=\sqrt{AD^2-DE^2}=\sqrt{5^2-4^2}=3\)
Vì ABCD là hình thang cân nên AE = FB = 3.
Suy ra AB = EF + AE + FB = 6 + 3 + 3 = 12.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.DE=\dfrac{12+6}{2}.4=36\left(cm^2\right)\)

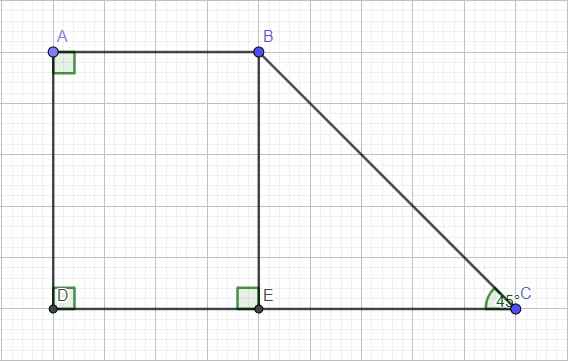
Kẻ đường cao BE ứng với CD \(\Rightarrow BE=4\left(cm\right)\)
Trong tam giác vuông BCE ta có:
\(\widehat{EBC}=90^0-\widehat{C}=90^0-45^0=45^0\)
\(\Rightarrow\widehat{EBC}=\widehat{C}\Rightarrow\Delta BCE\) vuông cân tại E
\(\Rightarrow EC=BE=4\left(cm\right)\)
Tứ giác ABED là hình chữ nhật (tứ giác có 3 góc vuông)
\(\Rightarrow AB=DE\)
Ta có:
\(AB+CD=10\left(cm\right)\)
\(\Leftrightarrow AB+DE+EC=10\)
\(\Leftrightarrow2AB+4=10\)
\(\Rightarrow AB=3\left(cm\right)\)
\(\Rightarrow DE=AB=3cm\Rightarrow CD=DE+EC=7\left(cm\right)\)