Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.png)
Xét tứ giác AMCN có AM song song và bằng CN nên nó là hình bình hành.
Suy ra AN song song và bằng MC.
Xét tam giác DMH và tam giác BNI có:
DM = BN
\(\widehat{MDH}=\widehat{NBI}\) (So le trong)
\(\widehat{DMH}=\widehat{BNI}\) (Cùng bằng góc \(\widehat{HCN}\))
\(\Rightarrow\Delta DMH=\Delta BNI\left(g-c-g\right)\)
\(\Rightarrow\) IN = HM
Vậy nên AI = HC.
Từ đó ta có AI = AN - IC = MC - MH = HC.
Xét tứ giác AICH có AH song song và bằng IC nên AICH là hình bình hành. Suy ra AH = IC.
Ta thấy ngay trong tam giác DIC, HF là đường trung bình. Vậy thì HF song song và bằng một nửa IC. Tương tự EI song song và bằng một nửa AH. Vậy nên EIFH là hình bình hành.
Để hình bình hành EIFH là hình chữ nhật thì EF = HI.
Xét tam giác BHC có N là trung điểm BC, IN // HC nên IN là đường trung bình của tam giác. Vậy thì IB = HI.
Tương tự HI = DH.
Từ đó ta có IH = BD/3
Mà EF = BC nên để EIFH là hình chữ nhật thì hình bình hành ABCD có BD = 3BC.
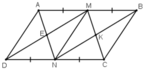
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC;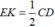 
(vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
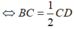
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.
Câu 1:
a)
\(BM=MC=\frac{1}{2}BC\) (M là trung điểm của BC)
\(AN=ND=\frac{1}{2}AD\) (N là trung điểm của AD)
mà \(BC=AD\) (ABCD là hình bình hành)
\(\Rightarrow AN=ND=BM=MC\) (1)
mà ND // BM
=> BMDN là hình bình hành
=> BN // MD (2)
=> MDKB là hình thang
b)
MC = AN (theo 1)
mà MC // AN (ABCD là hình bình hành)
=> AMCN là hình bình hành
=> AM // CN (3)
Từ (2) và (3)
=> MPNQ là hình bình hành (4)
BM = AN (theo 1)
mà BM // AN (ABCD là hình bình hành)
=> ABMN là hình bình hành
mà AB = BM \(\left(=\frac{1}{2}BC\right)\)
=> ABMN là hình thoi
=> AM _I_ BN
=> MPN = 900 (5)
Từ (4) và (5)
=> MPNQ là hình chữ nhật
c)
MPNQ là hình vuông
<=> MN là tia phân giác của PMQ
mà MN là đường trung tuyến của tam giác MDA vuông tại M (N là trung điểm của AD; MPNQ là hình chữ nhật)
=> Tam giác MDA vuông cân tại M có MN là đường trung tuyến
=> MN là đường cao của tam giác MDA
=> MNA = 900
mà MNA = ABM (ABMN là hình thoi)
=> ABM = 900
mà ABCD là hình bình hành
=> ABCD là hình chữ nhật
Câu 2:
a)
\(AE=EB=\frac{AB}{2}\) (E là trung điểm của của AB)
\(CF=FD=\frac{CD}{2}\) (F là trung điểm của của CD)
mà AB = CD (ABCD là hình bình hành)
=> AE = EB = CF = FD (1)
mà AE // CF (ABCD là hình bình hành)
=> AECF là hình bình hành
b)
AE = FD (theo 1)
mà AE // FD (ABCD là hình bình hành)
=> AEFD là hình bình hành
mà DA = AE \(\left(=\frac{1}{2}AB\right)\)
=> AEFD là hình thoi
=> AF _I_ ED
=> EMF = 900 (2)
EB = FD (theo 1)
mà EB // FD (ABCD là hình bình hành)
=> EBFD là hình bình hành
=> EM // NF
mà EN // MF (AECF là hình bình hành)
=> EMFN là hình bình hành
mà EMF = 900 (theo 2)
=> EMFN là hình chữ nhật
c)
EMFN là hình vuông
<=> EF là tia phân giác của MEN
mà EF là đường trung tuyến của tam giác ECD vuông tại E (F là trung điểm của CD; EMFN là hình chữ nhật)
=> Tam giác ECD vuông cân tại E có EF là đường trung tuyến
=> EF là đường cao của tam giác ECD
=> EFD = 900
mà EFD = DAE (AEFD là hình thoi)
=> DAE = 900
mà ABCD là hình bình hành
=> ABCD là hình chữ nhật
Gọi O là giao điểm của AC, BD
Vì O là tâm đối xứng của hình bình hành nên ta có:
MN đi qua O và OM = ON
hiển nhiên O là trung điểm EF
=> MENF là hình bình hành (1)
mặt khác:
EF = FD = 2OF => OF = FD/2
từ AD = FD = BD/3 và ON là đường trung bình của tgiác ACD nên
ON = AD/2 = FD/2 = OF => MN = EF (2)
từ (1) và (2) => MENF là hình chữ nhật
b) MENF là hình vuông khi và chỉ khi hình chữ nhật MENF có 2 đường chéo vuông góc: MN vuông EF
<=> MN vuông BD <=> AD vuông BD
chúc you học tốt!! ^^
ok mk nha!!! 45464564556765587696532543545654645654645756756756756585634564634
bn đang hok lớp 8 ak giống mk!! ^^
76756768534556345634346654767567636456574675765
bạn xem lại đề 1 chút đi! hình như sai thứ tự điểm đó bạn! mk ko vẽ được hình