Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài giải:
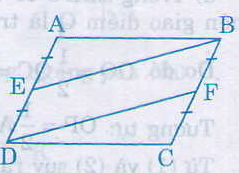
Tứ giác BEDF có:
DE // BF ( vì AD // BC)
DE = BF \(\left(DE=\dfrac{1}{2}AD=\dfrac{1}{2}BC=BF\right)\)
Nên BEDF là hình bình hành.
Suy ra BE = DF.
Xét \(\Delta ABF\) và \(\Delta CDE\) có :
\(AB=CD\left(gt\right)\)
Góc \(A\) \(=\) Góc \(B\) \((gt)\)
\(AE=CF\left(=\dfrac{1}{2}AD=\dfrac{1}{2}BC\right)\)
Vậy \(\Delta ABE=\Delta CDF\left(c.g.c\right)\)
\(\Rightarrow BE=DF\) (2 cạnh tương ứng)
P/s : Đây là lần đầu em vẽ hình trên máy nên dễ sai sót ạ,với lại em khong thấy kí hiệu góc ở đâu ạ :v Thông cảm cho em

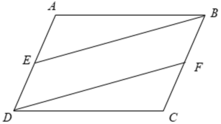
Xét tứ giác BEDF có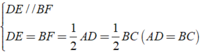
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên
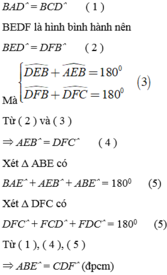

a) Ta chứng minh được BEDF là hình bình hành Þ BE = DF và E B F ^ = C D F ^ .
Cách khác: DAEB = DCFD (c.g.c) suy ra BE = DF và A B E ^ = C D F ^ .

b) Vì BEDF hình bình hành Þ ĐPCM

Bài này có 2 cách nha bạn
Cách 1:
+ ABCD là hình bình hành => AB = CD, AD = BC, \(\widehat{A}=\widehat{C}\)
+ E là trung điểm của AD \(\Rightarrow AE=\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow CF=\frac{BC}{2}\)
Mà AD = BC (cmt) => AE = CF.
+ Xét ΔAEB và ΔCFD có: AB = CD, \(\widehat{A}=\widehat{C}\), AE = CF (cmt)
=> ΔAEB = ΔCFD (c.g.c)
=> EB = DF.
Cách 2:
ABCD là hình bình hành => AD//BC và AD = BC.
+ AD // BC => DE // BF
+ E là trung điểm của AD \(\Rightarrow DE=\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow BF=\frac{BC}{2}\)
Mà AD = BC => DE = BF.
+ Tứ giác BEDF có:
DE // BF và DE = BF
=> BEDF là hình bình hành
=> BE = DF

mk sửa lại đề nha: chứng minh rằng BE = DF
ABCD là hình bình hành \(\Rightarrow\)AB = CD; AD = BC; \(\widehat{A}\)= \(\widehat{C}\)
E là trung điểm AD \(\Rightarrow\)EA = \(\frac{AD}{2}\)
F là trung điểm BC \(\Rightarrow\)CF = \(\frac{BC}{2}\)
mà AD = BC nên AE = CF
Xét \(\Delta\)AEB và \(\Delta\)CFD có:
AB = CD (cmt)
\(\widehat{A}\)= \(\widehat{C}\) (cmt)
AE = CF (cmt)
suy ra; \(\Delta\)AEB = \(\Delta\)CFD (c.g.c)
suy ra BE = DF (2 cạnh tương ứng)

mình gợi ý cho bạn là ra ngay nhé ! bạn hãy nhớ kiến thức chứng minh tam giác bằng nhau và dùng sơ đồ tư duy ạ ! bài này chứng minh cặp tam giác EBF và EFD sẽ có EF chung , ED=BF vì E là TĐ AD thì EA=ED ; F là TĐ BC thì FB=FC , mà AD =BC thì 2 cạnh đối của HBH , lại thấy AD//BC ( tính chất của HBH) =>> góc FED=góc BFE (slt)
bài này rất dễ ra nếu bạn nắm chắc kiến thức cơ bản , lí thuyết của bài HBH nhé !
Mình gợi ý như vậy chắc bạn ra rồi ! good luck !
ABCD là hình bình hành => AB = CD ; góc A = góc C ; AD = BC
E là trung điểm AD \(\Rightarrow\)\(AE=\frac{AD}{2}\)
F là trung điểm của BC \(\Rightarrow\)\(FC=\frac{BC}{2}\)
Mà AD = BC
Nên AE = FC
Xét \(\Delta ABE\)và \(\Delta CDF\)
\(\widehat{A}=\widehat{C}\)
\(AE=FC\)( cmt )
\(AB=CD\)( cmt )
\(\Rightarrow\)\(\Delta ABE=\Delta CDF\left(c-g-c\right)\)
\(\Rightarrow\)\(BE=DF\)( đpcm )
Cách 1:
+ ABCD là hình bình hành ⇒ AB = CD, AD = BC, Â = Ĉ.
+ E là trung điểm của AD ⇒ AE = AD/2
F là trung điểm của BC ⇒ CF = BC/2
Mà AD = BC (cmt) ⇒ AE = CF.
+ Xét ΔAEB và ΔCFD có: AB = CD, Â = Ĉ, AE = CF (cmt)
⇒ ΔAEB = ΔCFD (c.g.c)
⇒ EB = DF.
Cách 2:
ABCD là hình bình hành ⇒ AD//BC và AD = BC.
+ AD // BC ⇒ DE // BF
+ E là trung điểm của AD ⇒ DE = AD/2
F là trung điểm của BC ⇒ BF = BC/2
Mà AD = BC ⇒ DE = BF.
+ Tứ giác BEDF có:
DE // BF và DE = BF
⇒ BEDF là hình bình hành
⇒ BE = DF.