Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

V ( C ; 2 ) ( I G H F ) = ( A I F D ) ; Đ I ( A I F D ) = C I E B .
Đáp án C.

Đáp án A
B = V A ; k ( M ) và 2 M A → = A B →
C = V A ; k ( N ) và 2 N A → = A C →
=>k = 2

Gọi A’ là điểm đối xứng với A qua tâm O.
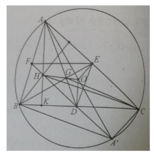
chứng minh BHCA’ là hình bình hành, suy ra H, A', D thẳng hàng và DO là đường trung bình của tam giác AHA’ ⇒ D O → = - 1 / 2 A H → ⇒ phép vị tự tâm G tỉ số -1/2 biến A H → thành DO → .
Đáp án B

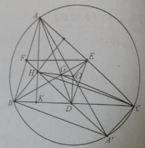
Phép vị tự tâm G tỉ số -1/2 biến A thành D; biến B thành E; biến C thành F ⇒ biến tam giác ABC thành tam giác DEF.
Đáp án B

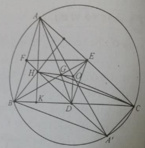
G D → = - 1 / 2 G A → ⇒ phép vị tự tâm G tỉ số -1/2 biến A thành D.
Đáp án B.

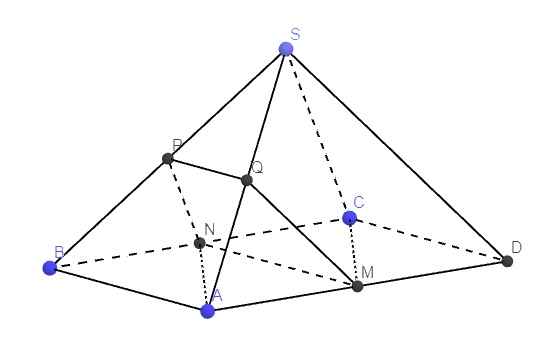
a. Do M, N là trung điểm AD, BC \(\Rightarrow MN||AB||CD\)
Gọi Q là trung điểm SA
\(\Rightarrow PQ\) là đường trung bình tam giác SAB
\(\Rightarrow PQ||AB\Rightarrow PQ||MN\Rightarrow Q\in\left(MNP\right)\)
\(\Rightarrow Q=SA\cap\left(MNP\right)\)
b. Do Q là trung điểm SA, M là trung điểm AD
\(\Rightarrow MQ\) là đường trung bình tam giác SAD \(\Rightarrow MQ||SD\)
Mà \(MQ\in\left(MNP\right)\Rightarrow SD||\left(MNP\right)\)
Tương tự ta có \(NP||SC\) (đường trung bình) (1)
\(\left\{{}\begin{matrix}AM=NC=\dfrac{1}{2}AD\\AM||NC\end{matrix}\right.\) \(\Rightarrow AN||CM\) (2)
(1);(2) \(\Rightarrow\left(SMC\right)||\left(ANP\right)\)
c. Đề bài không tồn tại điểm L
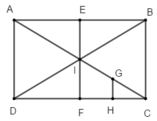
Đáp án B
B = V H ; k ( D ) và H B → = − 2 H D → => k=-2