Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
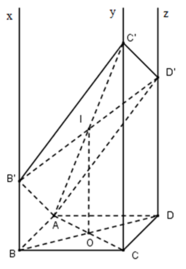
Trên Bx và Dz lấy điểm B′ và D′ sao cho BB’ = 2, DD’ =4
Gọi O là tâm hình bình hành ABCD, I là trung điểm của B′D′
Ta có BDD′B′ là hình thang, OI là đường trung bình của hình thang nên
OI // BB′ // DD′ // Cy
OI = B B ' + D D ' 2 = 2 + 4 2 = 3
Xét mặt phẳng tạo bởi OI và CC′ có: AI ∩ Cy = C′
Ta có OI // CC′, AO = OC suy ra AI = IC′
Suy ra OI là đường trung bình của tam giác ACC′ ⇒ CC′ = 2OI = 6
Đáp án cần chọn là: D

Đáp án C
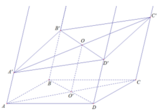
Trên Ax lấy điểm A’ sao cho AA’= x
Trên By lấy điểm B’ sao cho BB’ = y
Trên Cz lấy điểm C’ sao cho CC’ = z
Gọi α là mặt phẳng chứa tia Cz và Dt
Xét (A’B’C’) và α có:
C’ là điểm chung
A’B’ // α
⇒ giao tuyến của α và (A’B’D’) là đường thẳng d đi qua C’ và song song với A’B’
Trong mặt phẳng α , ta có: d cắt Dt tại D’
Gọi O = A C ∩ B D , O ' = A C ' ∩ B ' D '
Xét hình thang AA’C’C có: OO’ là đường trung bình
⇒ O O ' = A A ' + C C ' 2 = x + z 2
Xét tam giác BDD’D có: OO’ là đường trung bình
⇒ O O ' = D D ' + B B ' 2 ⇒ DD’ = x + z – y

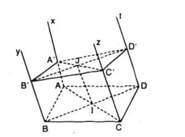
a) Do ABCD là hình bình hành, nên AB // DC
=> AB // (Cz, Dt) (1)
Theo giả thiết Ax // Dt nên Ax // (Cz, Dt) (2)
Từ (1) và (2) suy ra: (Ax, By) // (Cz, Dt)
b) Mặt phẳng β cắt 2 mặt phẳng song song ( Ax, By), (Cz, Dt) theo hai giao tuyến là A’B’và C’D’ nên A’B’// C’D’. (3)
Chứng minh tương tự (Ax, Dt) song song với (By,Cz).Và mặt phẳng β cắt 2 mặt phẳng song song (Ax, Dt), (By, Cz) theo hai giao tuyến là A’D’và B’C’ nên A’D’// B’C’ (4)
Từ (3) và (4) suy ra: tứ giác A’B’C’D’ là hình bình hành.
=> J là trung điểm của A’C’ ( tính chất hình bình hành).
Tứ giác AA’C’C là hình thang vì có: AA’ // CC’ ( giả thiết). Lại có, I và J lần lượt là trung điểm của AC và A’C’ nên IJ là đường trung bình của hình thang
=> IJ// AA’// CC’ ( đpcm).
c) Vì IJ là đường trung bình của hình thang ACC’A’ nên IJ = 1/2(AA’ + CC’)
IJ cũng là đường trung bình của hình thang BDD’B’: IJ = 1/2(BB’ + DD’)
Từ đây suy ra: DD’ + BB’ = AA’ + CC’
=> DD’ = AA’ + CC’ – BB’ = a + c – b

Đáp án B
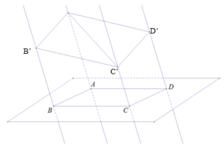
Giả sử mặt phẳng ban đầu là (A’B’C’). Ta cần xác định điểm D sao cho
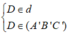
Xét (A’B’C’) và (C’CD) có:
C’ là điểm chung
A’B’//(C’CD) (do (A’B’BA) // (C’CD))
⇒ giao tuyến của (A’B’C’) và (C’CD) là đường thẳng m đi qua điểm C’ và song song với A’B’
⇒ m cắt d tại D’ là điểm cần tìm
Xét hình A’B’C’D’ có A’B’ // C’D’
⇒ A’B’ = C’D’ ( a, b, c, d là các đường thẳng song song lần lượt đi qua A, B, C, D là các đỉnh của hình bình hành)
⇒ A’B’C’D’ là hình bình hành

a) Có AA' // DD' và AB//DC nên \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\).
b) Do \(\left(Ax,By\right)\) // \(\left(C_z,D_t\right)\) và \(\left(\beta\right)\cap\left(AA'B'B\right)=A'B'\) và \(\left(\beta\right)\cap\left(CC'D'D\right)=C'D'\) nên \(A'B'\) // \(C'D'\).
Chứng minh tương tự B'C'//D'A'.
Do đó tứ giác A'B'C'D' là hình bình hành và J là trung điểm của A'C'.
Suy ra: IJ là đường trung bình của hình thang A'C'CA nên IJ // AA'.
c) Tương tự IJ là đường trung bình của hình thang B'D'DB \(IJ=\dfrac{\left(B'B+DD'\right)}{2}\).
Theo câu b IJ là đường trung bình của hình thang A'C'CA nên \(IJ=\dfrac{\left(AA'+CC'\right)}{2}\).
Suy ra: \(BB'+DD'=AA'+CC'\) hay \(DD'=a+c-b\).
Đáp án D
Trên Bx lấy điểm B’ sao cho BB’ = 4
Trên Dz lấy điểm D’ sao cho DD’ = 2
Gọi α là mặt phẳng chứa tia Bx và Dz
Xét (AB’D’) và α có:
B’ là điểm chung
AD’ // α
⇒ giao tuyến của α và (AB’D’) là đường thẳng d đi qua B’ và song song với AD’
Trong mặt phẳng α , ta có: d cắt Cz tại C’
Gọi O = A C ∩ B D , O ' = A C ' ∩ B ' D '
Xét hình thang BB’D’D có: OO’ là đường trung bình
Xét tam giác ACC’ có: OO’ là đường trung bình