Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

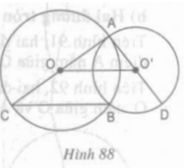
a) Hai đường tròn (O) và (O’) cắt nhau
b) Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.

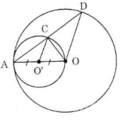
Gọi O’ là tâm của đường tròn đường kính OA.
Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Suy ra, hai đường tròn đã cho tiếp xúc trong với nhau.

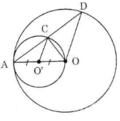
a) Gọi O’ là tâm của đường tròn đường kính OA.
Gọi R và r lần lượt là bán kính đường tròn tâm O và tâm O’.

Suy ra, hai đường tròn đã cho tiếp xúc trong với nhau.
b) +) Xét đường tròn (O’) có A, O, C là ba điểm cùng thuộc đường tròn và OA là đường kính nên tam giác AOC vuông tại C.
⇒ OC ⊥ AD
+) Xét đường tròn tâm (O) có A, D là hai điểm thuộc đường tròn nên OA = OD
⇒ ΔAOD cân tại O mà OC ⊥ AD
⇒ OC là đường trung tuyến của ΔAOD
⇒ C là trung điểm của AD
⇒ AC = CD

Hướng dẫn giải:

a) Gọi O' là tâm của đường tròn đường kính OA thì O'A=O'O.
Ta có OO'=OA-O'A hay d=R-r nên đường tròn (O) và đường tròn (O') tiếp xúc trong.
b) Tam giác CAO có cạnh OA là đường kính của đường tròn ngoại tiếp nên ΔCAO vuông tại C
⇒OC⊥AD
⇒CA=CD (đường kính vuông góc với một dây).

Gọi R là bán kính của đường tròn (O; 2). Ta có: R = 2
O A 2 = 1 2 + 1 2 = 2 ⇒ OA = 2 < 2
Vì OA < R nên điểm A nằm trong đường tròn (O; 2)
O B 2 = 2 2 + 2 2 = 2 + 2 = 4 ⇒ OB = 2
Vì OB = R nên điểm B thuộc đường tròn (O; 2)
O C 2 = 1 2 + 2 2 = 1 + 4 = 5 ⇒ OC = 5 > 2
Hai đường tròn (O) và (O’) cắt nhau