Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi phương trình đường thẳng d qua M, N có dạng \(y=ax+b\)
Do d qua \(A\left(1;2\right)\Rightarrow2=a+b\Rightarrow b=2-a\)
Phương trình d: \(y=ax-a+2\)
Tọa độ M là giao của d với Ox :
\(\Rightarrow y_M=0\Rightarrow0=ax_M-a+2\Rightarrow x_M=\frac{a-2}{a}\Rightarrow OM=\left|\frac{a-2}{a}\right|\)
Tọa độ N là giao của d với Oy
\(\Rightarrow x_N=0\Rightarrow y_N=0.a-a+2=-a+2\Rightarrow ON=\left|-a+2\right|=\left|a-2\right|\)
\(T=\frac{1}{OM^2}+\frac{1}{ON^2}=\frac{1}{\left(\frac{a-2}{a}\right)^2}+\frac{1}{\left(a-2\right)^2}=\frac{a^2+1}{\left(a-2\right)^2}=\frac{5a^2+5}{5\left(a-2\right)^2}\)
\(T=\frac{a^2-4a+4+4a^2+4a+1}{5\left(a-2\right)^2}=\frac{\left(a-2\right)^2+\left(2a+1\right)^2}{5\left(a-2\right)^2}=\frac{1}{5}+\frac{\left(2a+1\right)^2}{5\left(a-2\right)^2}\ge\frac{1}{5}\)
\(\Rightarrow T_{min}=\frac{1}{5}\) khi \(a=-\frac{1}{2}\)
Đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 - 2 2 nên ta có n = 1 - 2
Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2 + 2 nên ta có:
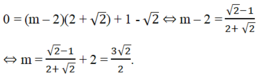
Trả lời: Khi n = 1 -
2
và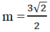 
thì đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 -
2
và cắt trục hoành tại điểm có hoành độ 2 +
2
