Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=-2 vào y=-3x+4, ta được:
y=6+4=10
Thay x=-2 và y=10 vào hàm số \(y=ax^2\), ta được:
\(4a=10\)
hay a=5/2
c: (P): y=5/2x2
(d): y=-3x+4
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{5}{2}x^2+3x-4=0\\y=-3x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x^2+6x-8=0\\y=-3x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x^2+10x-4x-8=0\\y=-3x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(5x-4\right)=0\\y=-3x+4\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;10\right);\left(\dfrac{4}{5};\dfrac{8}{5}\right)\right\}\)

a) Để đồ thị hàm số \(y=ax^2\) đi qua điểm A(4;4) thì
Thay x=4 và y=4 vào hàm số \(y=ax^2\), ta được:
\(a\cdot4^2=4\)
\(\Leftrightarrow a\cdot16=4\)
hay \(a=\dfrac{1}{4}\)
a, - Thay tọa độ điểm A vào hàm số ta được : \(4^2.a=4\)
\(\Rightarrow a=\dfrac{1}{4}\)
b, Thay a vào hàm số ta được : \(y=\dfrac{1}{4}x^2\)
- Ta có đồ thì của hai hàm số :
c, - Xét phương trình hoành độ giao điểm :\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x\)
\(\Leftrightarrow x^2+2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Vậy hai hàm số trên cắt nhau tại hai điểm : \(\left(0;0\right);\left(-2;1\right)\)

Tham khảo:


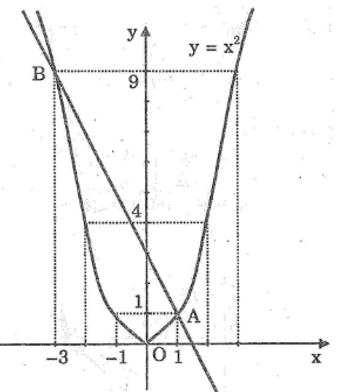
c. Giao điểm thứ hai của đồ thị có hoành độ bằng -3 và tung độ bằng 9. Ta có : B(-3 ; 9).

a) (d) cắt (P) tại A => A thuộc d và (P)
xA= 3; A \(\in\) d=> yA = -xA - \(\frac{3}{2}\) => yA = -3 - \(\frac{3}{2}\) = \(\frac{-9}{2}\)
Mặt khác, A \(\in\) (P) => yA = axA2 => \(\frac{-9}{2}\) = a. 32 => a = \(\frac{-9}{2}\): 9 = \(\frac{-1}{2}\)
Vậy (P) có dạng y = \(\frac{-1}{2}\).x2
+) Vẽ đồ thị:
| x | -2 | -1 | 0 | 1 | 2 |
| y | -2 | \(\frac{-1}{2}\) | 0 | \(\frac{-1}{2}\) | -2 |
(P) đí qua 4 điểm (-2;-2); (-1;\(\frac{-1}{2}\)); (0;0); (1;\(\frac{-1}{2}\)); (2;-2)
b) Phương trình hoành độ giao điểm: \(\frac{-1}{2}\).x2 = - x - \(\frac{3}{2}\)
<=> -x2 + 2x + 3 = 0
<=> x = -1 hoặc x = 3 (Vì a - b + c = -1 - 2 + 3 = 0)
=> xB = -1 => yB = \(\frac{-1}{2}\).(-1)2 = \(\frac{-1}{2}\)
Vậy B (-1;\(\frac{-1}{2}\))


a: Thay x=-2 vào y=-3x+4, ta được:
y=6+4=10
Thay x=-2 và y=10 vào hàm số \(y=ax^2\), ta được:
\(4a=10\)
hay a=5/2
c: (P): y=5/2x2
(d): y=-3x+4
Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{5}{2}x^2+3x-4=0\\y=-3x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x^2+6x-8=0\\y=-3x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}5x^2+10x-4x-8=0\\y=-3x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x+2\right)\left(5x-4\right)=0\\y=-3x+4\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(-2;10\right);\left(\dfrac{4}{5};\dfrac{8}{5}\right)\right\}\)