Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(h\left(x\right)=f\left(x^2+1\right)-m\Rightarrow h'\left(x\right)=2x.f'\left(x^2+1\right)\)
\(h'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\f'\left(x^2+1\right)=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x^2+1=2\\x^2+1=5\end{matrix}\right.\) \(\Rightarrow x=\left\{-2;-1;0;1;2\right\}\)
Hàm có nhiều cực trị nhất khi \(h\left(x\right)=m\) có nhiều nghiệm nhất
\(f\left(x\right)=\int f\left(x\right)dx=\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x+C\)
\(f\left(1\right)=0\Rightarrow C=-\dfrac{199}{12}\Rightarrow f\left(x\right)=-\dfrac{1}{4}x^4-\dfrac{5}{3}x^3-2x^2+20x-\dfrac{199}{12}\)
\(x=\pm2\Rightarrow x^2+1=5\Rightarrow f\left(5\right)\approx-18,6\)
\(x=\pm1\Rightarrow x^2+1=2\Rightarrow f\left(2\right)\approx6,1\)
\(x=0\Rightarrow x^2+1=1\Rightarrow f\left(1\right)=0\)
Từ đó ta phác thảo BBT của \(f\left(x^2+1\right)\) có dạng:
Từ đó ta dễ dàng thấy được pt \(f\left(x^2+1\right)=m\) có nhiều nghiệm nhất khi \(0< m< 6,1\)
\(\Rightarrow\) Có 6 giá trị nguyên của m
Đơn giản là bạn vẽ cái hàm bậc 4 đó ra và cho -m và -m-10 cắt thôi. Vì -m-10<-m nên -m-10 sẽ nằm ở dưới, còn -m nằm trên. Nên -m sẽ cắt 2 điểm và -m-10 cắt 4 điểm cho ta 6 điểm. Ngoài ra k còn trường hợp nào khác mà -m và -m-10 cắt thỏa mãn
có 3 điểm cực trị.
Chọn D
Xét hàm số 
.
Có 
.
Ta lại có 
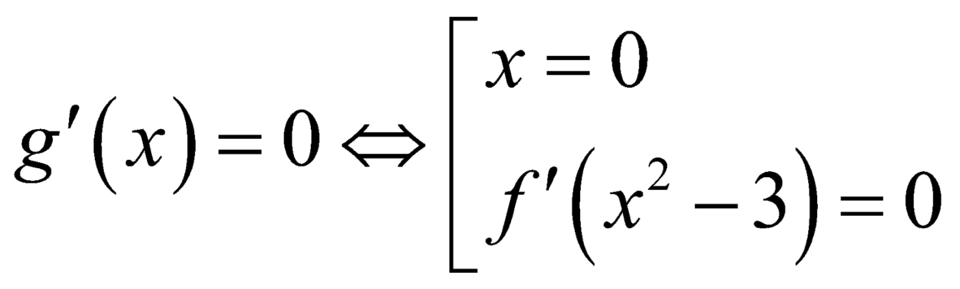
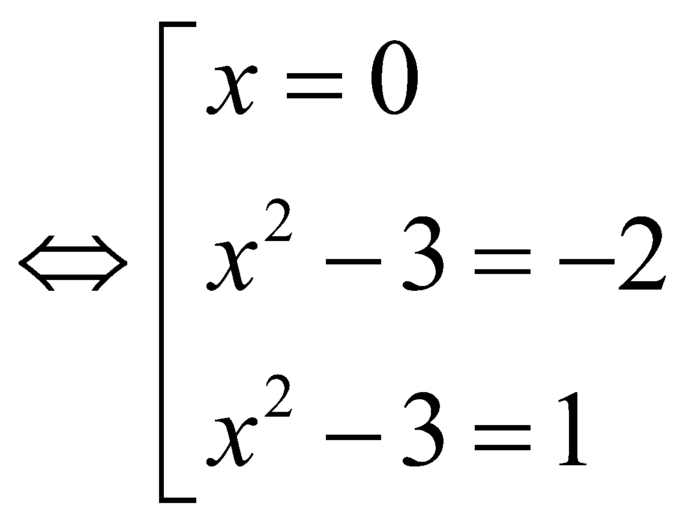
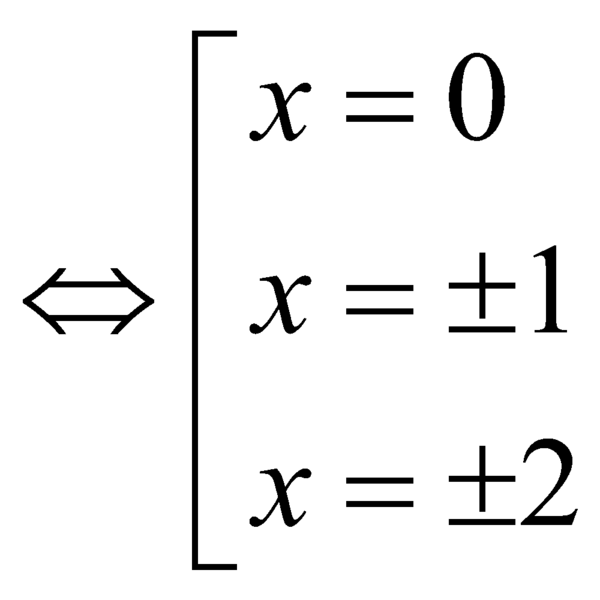thì 
. Do đó 
thì 
.
thì 
. Do đó 
thì 
.
Từ đó ta có bảng biến thiên của 
như sau
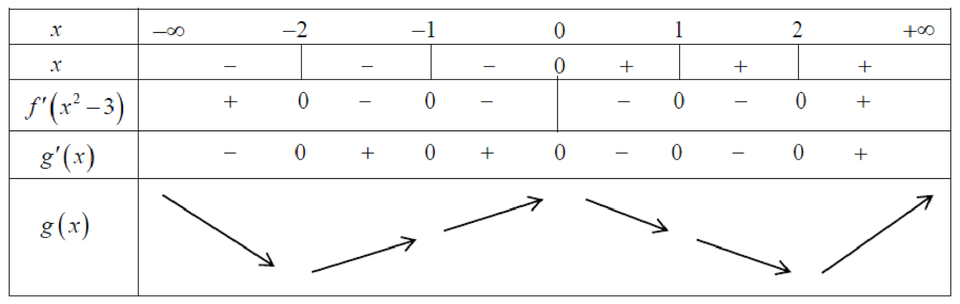
Dựa vào bảng biến thiên, ta có
I. Hàm số 
có 3 điểm cực trị . LÀ MỆNH ĐỀ ĐÚNG.
II. Hàm số 
đạt cực tiểu tại 
LÀ MỆNH ĐỀ SAI.
III. Hàm số 
đạt cực đại tại 
LÀ MỆNH ĐỀ SAI.
IV. Hàm số 
đồng biến trên khoảng 
LÀ MỆNH ĐỀ ĐÚNG.
V. Hàm số 
nghịch biến trên khoảng 
LÀ MỆNH ĐỀ SAI.
Vậy có hai mệnh đề đúng.
ở chỗ x<1=> x= -2 thì sao bạn ơi =>(x^2 -3) =1 >0 thì sao f ' (...)>0 được ????
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g\left(x\right)=f\left(x^2-2x\right)\)
\(g'\left(x\right)=2\left(x-1\right)f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
\(f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x^2-2x=-2\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
BBT:
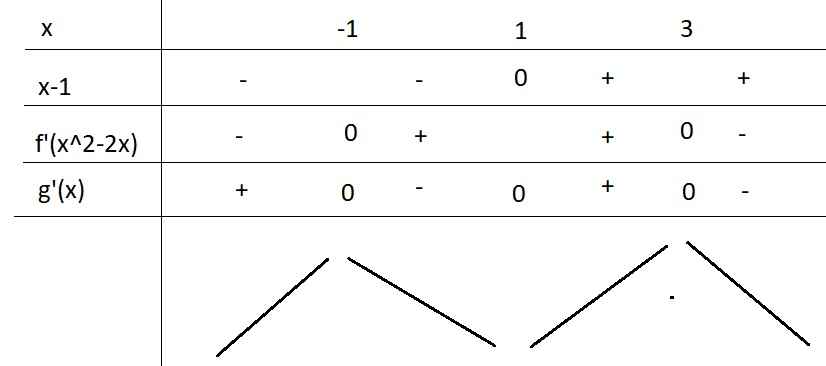
Từ BBT ta thấy \(f\left(x^2-2x\right)\) có 1 cực tiểu
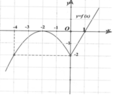
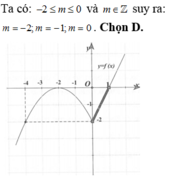
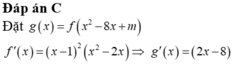
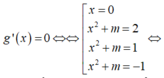
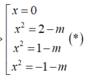
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
cho em hỏi là tại sao m≠0 mà đkxđ của m lại là -3<m<3 ạ ?