Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
PT có hai nghiệm thực phân biệt ⇔ m - 1 < 0 m - 1 > 4 ⇔ m < 1 m > 5

Đáp án C
f ( x ) − 1 = m ⇔ f ( x ) = m + 1 có hai nghiệm khi và chỉ khi m + 1 = − 1 m + 1 > 0 ⇔ m = − 2 m > − 1

Đáp án D.
P T f x = m vô nghiệm ⇔ − 2 ≤ m ≤ 1 ⇔ m ∈ − 2 ; 1 .
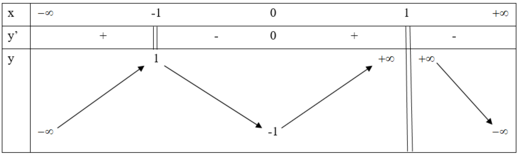

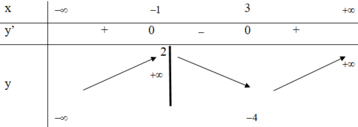

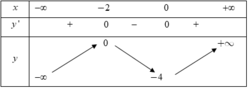
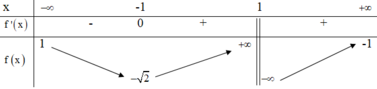
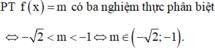

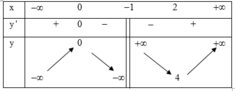
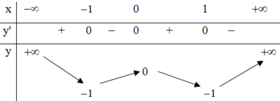
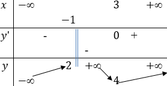

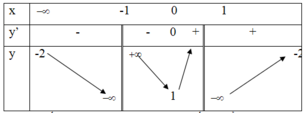
Phương pháp
Số nghiệm của phương trình f(x) = m là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m song song với trục hoành.
Cách giải
Số nghiệm của phương trình f(x) = m là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m song song với trục hoành.
Dựa vào BBT ta thấy, phương trình f(x) = m có đúng 3 nghiệm thực khi và chỉ khi m = ± 1
Vậy S = - 1 ; 1 .
Chọn B