Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
. 
Chọn D.
Xét I = ∫ 0 1 f ' x d x Đặt t = x → t 2 = x → 2 t d t = d x
Đổi cận x = 0 → t = 0 x = 1 → t = 1 . Khi đó I = 2 ∫ 0 1 t f ' ( t ) d t = 2 A
Tính A = ∫ 0 1 t f ' ( t ) d t . Đặt u = t d v = f ' t d t → d u = d t v = f t
Khi đó
.
.
.
.
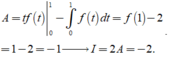
\(f'\left(x\right)=f'\left(1-x\right)\Rightarrow\int f'\left(x\right)dx=\int f'\left(1-x\right)dx\)
\(\Rightarrow f\left(x\right)=-f\left(1-x\right)+C\Rightarrow f\left(x\right)+f\left(1-x\right)=C\)
Thay \(x=0\Rightarrow f\left(0\right)+f\left(1\right)=C\Rightarrow C=42\)
\(\Rightarrow\int\limits^1_0\left[f\left(x\right)+f\left(1-x\right)\right]dx=\int\limits^1_042dx=42\)
Xét \(I=\int\limits^1_0f\left(1-x\right)dx\)
Đặt \(1-x=u\Rightarrow dx=-du;\left\{{}\begin{matrix}x=0\Rightarrow u=1\\x=1\Rightarrow u=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_1f\left(u\right).\left(-du\right)=\int\limits^1_0f\left(u\right).du=\int\limits^1_0f\left(x\right)dx\)
\(\Rightarrow2\int\limits^1_0f\left(x\right)dx=42\Rightarrow\int\limits^1_0f\left(x\right)dx=21\)
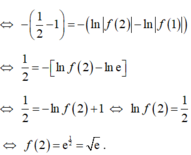
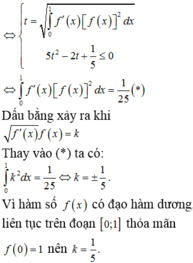
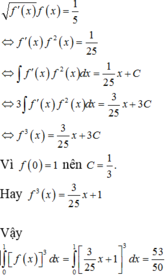
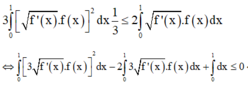
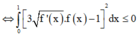
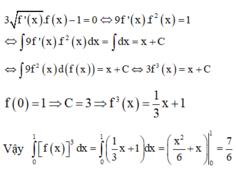
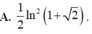
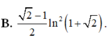
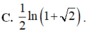
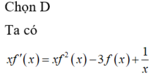
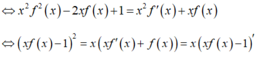
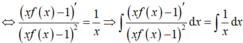
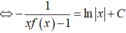
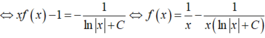
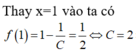
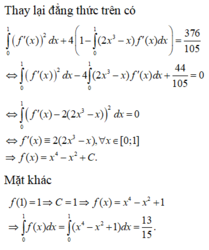
Đáp án B