Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
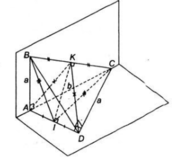
a: Gọi E là trung điểm của AB
ΔABC đều nên CE vuông góc AB
ΔABD đều nên DE vuông góc AB
=>AB vuông góc (CDE)
=>AB vuông góc CD
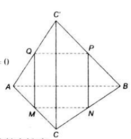
b: Xét ΔCAB có CN/CB=CM/CA
nên MN//AB và MN=1/2AB
Xét ΔDAB có DQ/DA=DP/DB
nên PQ//AB và PQ/AB=DQ/DA=1/2
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔADC có AQ/AD=AM/AC
nên QM//DC
=>QM vuông góc AB
=>QM vuông góc QP
=>MNPQ là hình chữ nhật
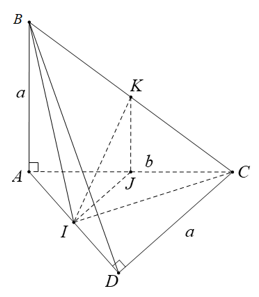
Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.
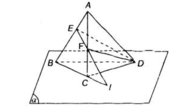
a) E ∈ AB mà AB ⊂ (ABC)
⇒ E ∈ (ABC)
F ∈ AC mà AC ⊂ (ABC)
⇒ F ∈ (ABC)
Đường thẳng EF có hai điểm E, F cùng thuộc mp(ABC) nên theo tính chất 3 thì EF ⊂ (ABC).
b) I ∈ BC mà BC ⊂ (BCD) nên I ∈ (BCD) (1)
I ∈ EF mà EF ⊂ (DEF) nên I ∈ (DEF) (2)
Từ (1) và (2) suy ra I là điểm chung của hai mặt phẳng (BCD) và (DEF).
a.
Trong mp (SAB) nối PM kéo dài cắt SB tại G
Trong mp (ABCD) nối PN cắt BC kéo dài tại H
\(\Rightarrow GH=\left(MNP\right)\cap\left(SBC\right)\)
b.
Nối SE cắt AD tại I, nối SF cắt BC tại K
Trong mp (ABCD), nối IK cắt PN kéo dài tại S
Trong mp (SBC), SF kéo dài cắt GH tại R
\(\Rightarrow RS\) là giao tuyến của (MNP) và (SEF)
Trong mp (SEF), nối RS và EF cắt nhau tại Q
\(\Rightarrow Q=EF\cap\left(MNP\right)\)
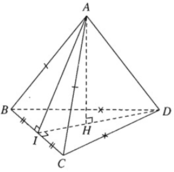
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).
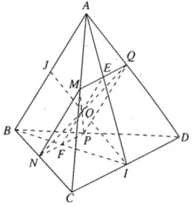
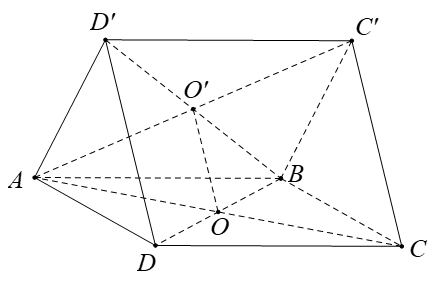
a)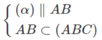 
⇒ (α) ∩ (ABC) = MN và MN // AB
Ta có N ∈ (BCD) và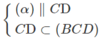 
Nên ⇒ (α) ∩ (BCD) = NP và NP // CD
Ta có P ∈ (ABD)
Và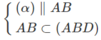 
nên ⇒ (α) ∩ (ABD) = PQ và PQ // AB
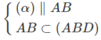nên ⇒ (α) ∩ (ACD) = MQ và MQ // CD
Do đó MN // PQ và NP // MQ, Vậy tứ giác MNPQ là hình bình hành.
b) Ta có: MP ∩ NQ = O. Gọi I là trung điểm của CD.
Trong tam giác ACD có : MQ // CD ⇒ AI cắt MQ tại trung điểm E của MQ.
Trong tam giác ACD có : NP // CD ⇒ BI cắt NP tại trung điểm F của NP.
Vì MNPQ là hình bình hành nên ta có
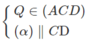
EF // MN ⇒ EF // AB
Trong ΔABI ta có EF // AB suy ra : IO cắt AB tại trung điểm J
⇒ I, O, J thẳng hàng
⇒ O ∈ IJ cố định.
Vì M di động trên đoạn AC nên Ochạy trong đoạn IJ .
Vậy tập hợp các điểm O là đoạn IJ.
