Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cần hình ib mình mình gửi cho nhé =)
a)
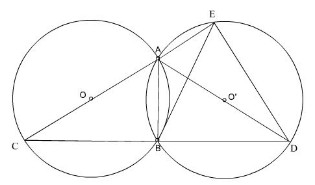
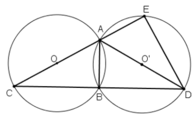
Vì (O) và (O′) cắt nhau tại hai điểm A và B nên OO′ vuông AB ( định lý )
- Xét tam giác ADC
Có OO′ là đường trung bình ( vì O là trung điểm AC , O′ là trung điểm của AD)
Nên => OO′ // CD
=> AB vuông CD ( Quan hệ từ vuông góc đến song song )
Xét tam giác ADC
Có AC = AD ( vì hai đường tròn (O) và (O′) có cùng bán kính )
=> Tam giác ACD cân tại A có AB là đường cao nên AB cũng là đường trung tuyến
=> BC = BD hay cung BC = cung BD (vì (O) và (O′) là hai đường tròn bằng nhau )
b) Xét đường tròn (O′) có A , E , D cùng thuộc đường tròn và AD là đường kính nên tam giác AED vuông tại E
\(\Rightarrow DE\perp AC\Rightarrow\widehat{DEC}=90^o\)
- Xét \(\Delta DEC\)vuông tại E có B là trung điểm DC ( cmt )
\(\Rightarrow EB=\frac{DC}{2}=BD=EB\)
=> Cung EB = cung BD ( định lý )
Do đó B là điểm chính giữa cung ED
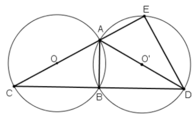
a) Nối C đến D.
Ta có 2 đường tròn bằng nhau => AC = AD
=> ∆ ACD cân tại A
Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )
Tương tự có góc ABD = 90°
=> ABC + ABD = 180°
=> C; B; D thẳng hàng và AB ⊥ CD
=> BC = BD
=> cung BC = cung BD
b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )
=> BH // EC
Mà theo (a) ta có BE = BD
=> BH là đường trung bình tam giác CDE
=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD
a) Nối C đến D.
Ta có 2 đường tròn bằng nhau => AC = AD
=> ∆ ACD cân tại A
Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )
Tương tự có góc ABD = 90°
=> ABC + ABD = 180°
=> C; B; D thẳng hàng và AB ⊥ CD
=> BC = BD
=> cung BC = cung BD
b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )
=> BH // EC
Mà theo (a) ta có BE = BD
=> BH là đường trung bình tam giác CDE
=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD
a) Nối C đến D.
Ta có 2 đường tròn bằng nhau => AC = AD
=> ∆ ACD cân tại A
Lại có góc ABC = 90°; do có OB = OC = OA = R ( tính chất trung tuyến ứng với cạnh huyền )
Tương tự có góc ABD = 90°
=> ABC + ABD = 180°
=> C; B; D thẳng hàng và AB ⊥ CD
=> BC = BD
=> cung BC = cung BD
b) Nối E đến D; từ B hạ BH ⊥ ED Ta có góc DEA = 90° ( chứng minh tương tự theo (a) )
=> BH // EC
Mà theo (a) ta có BE = BD
=> BH là đường trung bình tam giác CDE
=> HE = HD mà BH ⊥ ED => B là điểm chính giữa cung EBD
Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)
=> Tam giác AED vuông tại E
⇒ 
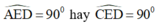
⇒ ΔECD vuông tại E.
Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )
⇒ EB = BD (CD/2).
⇒ 
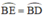(định lý) hay B là điểm chính giữa cung 
A) 2 tam giác vuông ABC,ABD bằng nhau ( vì cạnh huyền bằng nhau và cạnh góc vuông AB chung)
<=> CB=BD
Do 2 đường tròn (O) ; (O') bằng nhau nên
\(\widebat{BC}=\widebat{BD}\)
B) E nằm trên đường tròn đường kính AD nên
\(\widebat{AED}=90^0\)
Vì BC=BD (ở trên)
NênEB là trung tuyến của tam giác ECD vuông tại E
Từ đó,ta có : EB=ED
Vậy \(\widebat{BE}=\widebat{BD}\)và B là điểm chính giữa cung \(\widebat{EBD}\)
a) Vì \(A,B,C\in O\)
=> BO = OA = OC
\(\Rightarrow BO=\frac{AC}{2}\)
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí )
\(\Rightarrow\widehat{ABC}=90^o\)
Chứng minh tương tự :
\(\Rightarrow\widehat{ABD}=90^o\)
Đường tròn tâm O và O’ bằng nhau
=> AC = AD ( AC , AD lần lượt là bán kính của (O) và (O’) )
Xét hai tam giác vuông ABC và ABD có:
AB chung , AC = AD
\(\Rightarrow\Delta ABC=\Delta ABD\left(ch-cgv\right)\)
=> BC = BD ( 2 cạnh tương ứng )
\(\Rightarrow\widebat{BC}=\widebat{BD}\)( định lí )
Làm được mỗi câu a) ;-; thông kảm
Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒ 
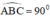
Chứng minh tương tự
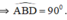
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒ 
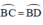( định lý )
a) Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒
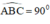
Chứng minh tương tự
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒
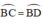( định lý )
b) Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)
=> Tam giác AED vuông tại E
⇒
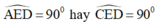
⇒ ΔECD vuông tại E.
Ta có:
Suy ra: C, B, D thẳng hàng.
Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )
⇒ EB = BD (CD/2).
⇒
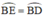(định lý) hay B là điểm chính giữa cung 
Kiến thức áp dụng
+ Với hai cung nhỏ trong cùng một đường tròn hoặc hai đường tròn bằng nhau thì hai dây bằng nhau căng hai cung bằng nhau.