Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(R_1+R_2=\dfrac{12}{0,3}=40\)
\(\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{12}{1,6}=7,5\Rightarrow R_1\cdot R_2=7,5\cdot40=300\)
\(\Rightarrow\left\{{}\begin{matrix}R_1=30\Omega\\R_2=10\Omega\end{matrix}\right.\) (ÁP DỤNG vI-ÉT LÀ RA)
Nối tiếp: \(R=U:I=12:0,3=40\Omega\)
Song song: \(R_{ss}=U:I_{ss}=12:1,6=7,5\Omega\)
\(\left\{{}\begin{matrix}R1ntR2\Rightarrow R=R1+R2=40\Omega_{\left(1\right)}\\R1//R2\Rightarrow R_{ss}=\dfrac{R1\cdot R2}{R1+R2}=7,5\Omega_{\left(2\right)}\end{matrix}\right.\)
Từ (1) và (2) \(\Rightarrow R1=10\Omega-R2=30\Omega\)

a. \(R_1=\dfrac{U}{I_1}=\dfrac{12}{0,6}=20\Omega\)
\(R_2=\dfrac{U}{I_2}=\dfrac{12}{0,4}=30\Omega\)
\(R_{AB}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{20.30}{20+30}=12\Omega\)
b. Điện trở bóng đèn là: \(R_đ=\dfrac{U^2}{P}=\dfrac{6^2}{3,6}=10\Omega\)
Cường độ định mức bóng đèn là: \(I_{đm}=\dfrac{P}{U}=\dfrac{3,6}{6}=0,6A\)
Cường độ dòng điện qua mạch AB là: \(I=\dfrac{U}{R_đ+R_{12}}=\dfrac{12}{10+12}=0,55A\)
Vì \(I< I_{đm}\) nên đèn sáng yếu hơn bình thường
c. Nhiệt lượng tỏa ra toàn mạch trong 15 phút là: \(Q=I^2Rt=0,55.\left(12+10\right).15.60=10890J\)

Khi R1 mắc nối tiếp với R2 thì: 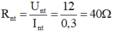 ↔ R1 + R2 = 40Ω (1)
↔ R1 + R2 = 40Ω (1)
Khi R1 mắc song song với R2 thì:
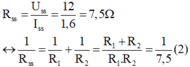
Thay (1) vào (2) ta được R1.R2 = 300
Ta có: R2 = 40 – R1 → R1.(40 – R1) = 300 ↔ - R12 + 40R1 – 300 = 0 (*)
Giải (*) ta được: R1 = 30Ω; R2 = 10Ω hoặc R1 = 10Ω; R2 = 30Ω.

R 1 + R 2 = U / I = 40 ( R 1 . R 2 ) / ( R 1 + R 2 ) = U / I ’ = 7 , 5
Giải hệ pt theo R 1 ; R 2 ta được R 1 = 30 ; R 2 = 10
Hoặc R 1 = 10 ; R 2 = 30

\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}=\dfrac{3}{10}\Omega\)
\(\Rightarrow R_{tđ}=\dfrac{10}{3}\Omega\)
\(U_1=U_2=U_3=U=12V\)
\(I=\dfrac{U}{R}=\dfrac{12}{\dfrac{10}{3}}=3,6A\)
\(I_1=I_2=I_3=\dfrac{U_1}{R_1}=\dfrac{12}{10}=1,2A\)
Nếu mắc nối tiếp:
\(R_{tđ}=R_1+R_2+R_3=10+10+10=30\Omega\)
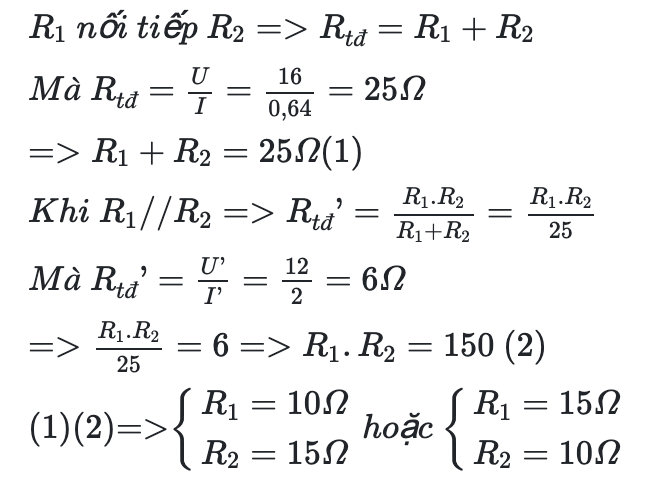
\(\Rightarrow\left\{{}\begin{matrix}R1ntR2\Rightarrow Rtd=R1+R2=\dfrac{U}{I}=\dfrac{16}{0,64}=25\left(\Omega\right)\left(1\right)\\R1//R2\Rightarrow Rtd=\dfrac{R1.R2}{R1+R2}=\dfrac{U'}{I'}=\dfrac{12}{2}=6\left(\Omega\right)\left(2\right)\\\end{matrix}\right.\)
\(\left(1\right)\left(2\right)\Rightarrow\left\{{}\begin{matrix}R1+R2=25\\\dfrac{R1R2}{R1+R2}=6\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}R2=25-R1\\\dfrac{R1\left(25-R1\right)}{R1+25-R1}=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}R2=25-R1\\-R1^2+25R1=150\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}R2=25-R1\\\left[{}\begin{matrix}R1=15\Omega\\R2=10\Omega\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}R1=15\Omega\\R2=25-15=10\Omega\end{matrix}\right.\\\left\{{}\begin{matrix}R1=10\Omega\\R2=15\Omega\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left(R1;R2\right)=\left\{\left(10;15\right);\left(15:10\right)\right\}\)