Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2
Kẻ D doi xung voi A qua Ox
E doi xung voi A qua Oy
Goi B' la 1 diem bat ki tren Ox,C' la 1 diem bat ki tren Oy
Do Ox la duong trung truc cua AD
=> BA=BD,B'A=B'A
Tuong tu=> C'A=C'E,CA=CE
Ta co
PABC=AB+BC+AC
Ma AB=BD.AC=CE
=>PABC=BC+BD+CE=ED
lai co B'D+B'E\(\ge ED\)
B'C'\(\ge B'E\)
=> B'D+B'C'+C'E\(\ge ED\)
=>PAB'C'\(\ge P_{ABC}\)
Dau ''='' xay ra khi B'\(\equiv B,C'\equiv C\)

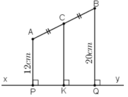
Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.
+ AP ⊥ xy và BQ ⊥ xy ⇒ AP // BQ
⇒ Tứ giác ABQP là hình thang.
+ CK ⊥ xy ⇒ CK // AP//BQ
+ Hình thang ABQP có AC = CB (gt) và CK // AP // BQ
⇒ PK = KQ
⇒ CK là đường trung bình của hình thang
⇒ CK = (AP + BQ)/2.
Mà AP = 12cm, BQ = 20cm ⇒ CK = 16cm.
Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm.

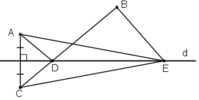
a) + A và C đối xứng qua d
⇒ d là trung trực của AC
⇒ AD = CD
⇒ AD + DB = CD + DB = CB (1)
+ E ∈ d ⇒ AE = CE
⇒ AE + EB = CE + EB (2)
+ CB < CE + EB (3)
Từ (1), (2), (3) ⇒ AD + DB < AE + EB
b) Vì với mọi E ∈ d thì AE + EB > AD + DB
Do đó con đường ngắn nhất bạn Tú nên đi là đường ADB.

Vì A' đối xứng với A qua xy
⇒ xy là đường trung trực của AA'.
⇒ CA' = CA (t/chất đường trung trực)
MA' = MA (t/chất đường trung trực)
AC + CB = A'C + CB = A'B (1)
MA + MB = MA'+ MB (2)
Trong ∆ MA'B, ta có:
A'B < A'M + MB (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB