Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (Làm như toán tổng tỉ)
Ta có: \(\widehat{xOy}+\widehat{yOz}=180\)độ (kề bù)
\(\Rightarrow\widehat{xOy}=180:\left(2+1\right)\times2=120\)độ
\(\Rightarrow\widehat{yOz}=180-120=60\)độ
b) Vì \(Om\)là phân giác \(\widehat{xOy}\Rightarrow\widehat{xOm}=\widehat{yOm}=\widehat{xOy}:2=120:2=60\)độ (Thật ra chỗ này còn cách khác nhưng thôi xài cái này đi ha!)
\(On\)là phân giác \(\widehat{yOz}\Rightarrow\widehat{yOn}=\widehat{nOz}=\widehat{yOz}:2=60:2=30\)độ
Ta có: \(\widehat{mOy}+\widehat{yOn}=\widehat{mOn}\)
\(\Rightarrow60+30=90\)độ (góc vuông)


Ta có : góc xOy + góc yOz = 180 ﴾kề bù﴿ => góc xOy + góc yOz = 90
=> góc yOm + góc yOn = 90 hay góc mOn = 90

a) \(\widehat{xOm}=\widehat{mOy}=\dfrac{\widehat{xOy}}{2}=\dfrac{62^0}{2}=31^0\)
\(\widehat{yOn}=\widehat{nOz}=\dfrac{180^0-62^0}{2}=90^0-31^0=59^0\)
b) \(\widehat{mOz}=\widehat{zOy}+\widehat{yOm}\)
\(=180^0-62^0+31^0\)
\(=118^0+31^0=149^0\)
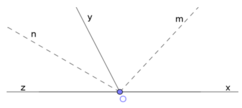

a,Ta có :\(\widehat{xOy}\)và \(\widehat{yOz}\)kề bù ( gt )
\(\Rightarrow\widehat{xOy}+\widehat{yOz}=180^0\)
Mà \(\widehat{xOy}=2\widehat{yOz}\left(gt\right)\)
\(\Rightarrow\widehat{xOy}-180^0:3.2=120^0\)
\(\Rightarrow\widehat{yOz}=180^0-120^0=60^0\)
b,Ta có:
Om là tia phân giác \(\widehat{xOy}\)
\(\Rightarrow\widehat{xOm}=\widehat{mOy}=\frac{\widehat{xOy}}{2}=60^0\)
On là tia phân giác \(\widehat{yOz}\)
\(\Rightarrow\widehat{zOn}=\widehat{nOy}=\frac{\widehat{yOz}}{2}=30^0\)
Tia Oy nằm giữa 2 tia Om và On
\(\Rightarrow\widehat{mOy}+\widehat{yOn}=\widehat{mOn}\)
\(60^0+30^0=\widehat{mOn}\)
\(\Rightarrow\widehat{mOn}=90^0\)
Như trên