Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

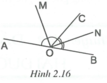
Ta có : \(\widehat{AOB}=160^0\)
Vì \(OM\)vuông góc với \(OA\)
=> \(\widehat{AOM}=90^0\)
Vậy \(\widehat{BOM}+\widehat{MOA}=\widehat{BOA}\)
\(\Rightarrow\widehat{BOM}=\widehat{BOA}-\widehat{MOA}\)
\(\widehat{BOM}=160^0-90^0\)
\(\widehat{BOM}=70^0\)
Theo ta thấy trên góc AOM có N nằm giữa
\(\Rightarrow\widehat{AON}=\widehat{\frac{AOM}{2}}=\frac{90^0}{2}=45^0\)
Đủ điều kiện chứng minh
\(\Rightarrow\widehat{AON}+\widehat{MON}=\widehat{AOM}\)
\(\widehat{MON}=\widehat{AOM}-\widehat{AON}\)
\(\widehat{MON}=90^0-45^0\)
\(\widehat{MON}=45^0\)
Vậy ....

Ta có O M ⊥ O N ⇒ M O N ^ = 90 ° .
Tia OM là tia phân giác của góc AOC nên A O M ^ = M O C ^ .
Tia ON là tia phân giác của góc BOC nên B O N ^ = N O C ^ .
Xét tổng
A O C ^ + B O C ^ = 2 M O C ^ + 2 N O C ^ = 2 M O C ^ + N O C ^ = 2 M O N ^ = 2.90 ° = 180 ° .
Hai góc kề AOC và BOC có tổng bằng nên hai tia OA, OB đối nhau.
Đường trung trực – Hai góc có cạnh tương ứng vuông góc
TA có MOA + MON + MOB =AOB = 160 độ
=> MOA + MON + MOB + MON - MON = 160 độ
=> AOM + BON - MON = 160 độ
=> 90 + 90 - MON = 160
=> MON = 180 - 160 = 20 độ
MON = 20 độ