
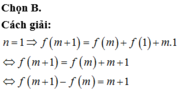
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

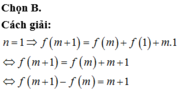
![]()
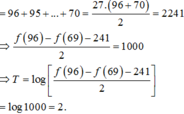

Đáp án B.
Cho m=1 ta có
f ( n + 1 ) = f ( n ) + f ( 1 ) + n ⇔ f ( n + 1 ) = f ( n ) + n + 1.
Khi đó
f ( 2 ) + f ( 3 ) + ... + f ( k ) = f ( 1 ) + 2 + f ( 2 ) + 3 + ... + f ( k − 1 ) + k + 1
⇔ f ( 2 ) + f ( 3 ) + ... + f ( k − 1 ) + f ( k ) = f ( 1 ) + f ( 2 ) + ... + f ( k − 1 ) + ( 1 + 2 + ... + k )
⇔ f ( k ) = f ( 1 ) + ( 1 + 2 + ... + k ) = 1 + k ( k + 1 ) 2 .
Vậy hàm cần tìm là
f ( x ) = 1 + x ( x + 1 ) 2 ⇒ f ( 96 ) = 1 + 96.97 2 = 4657 f ( 69 ) = 1 + 69.70 2 = 2416
Vậy
T = log 4657 − 2416 − 241 2 = log 1000 = 3.

Đáp án C
Ta có: f ' x = 2018. e x 2018 + e ' e x 2018 + e = e x 2018 e x 2018 + e = g x
Lại có: g a + g 2018 − a = e a 2018 e a 2018 + e + e 1 − a 2018 e 1 − a 2018 + e = e a 2018 e a 2018 + e + e e a 2018 + e = 1
Do đó T = g 1 + g 2017 + g 2 + g 2016 + ... + g 1010 + g 1009 = 1008 + g 1009
= 1008 + 1 2 = 2017 2 .