Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O đường kính AB vẽ tiếp tuyến Ax ,By với đường tròn tâm O . Lấy E trên nửa đường tròn , qua E vẽ tiếp tuyến với đường tròn cắt Ax tại D cắt By tại C
a, Chứng minh OADE nội tiếp được đường tròn
b, Nối AC cắt BD tại F , Chung minh EFsong song với AD
Câu hỏi tương tự Đọc thêmToán lớp 9
a: Xét tứ giác ADMO có
góc DAO+góc DMO=180 độ
nên ADMO là tứ giác nội tiếp
b: Gọi N là trung điểm của CD
Xét hình thang ABCD ccó
O,N lần lượt là trung điểm của AB,CD
nên ON là đường trung bình
=>ON//AD//BC
=>ON vuông góc với AB
=>AB là tiếp tuyến của (N)

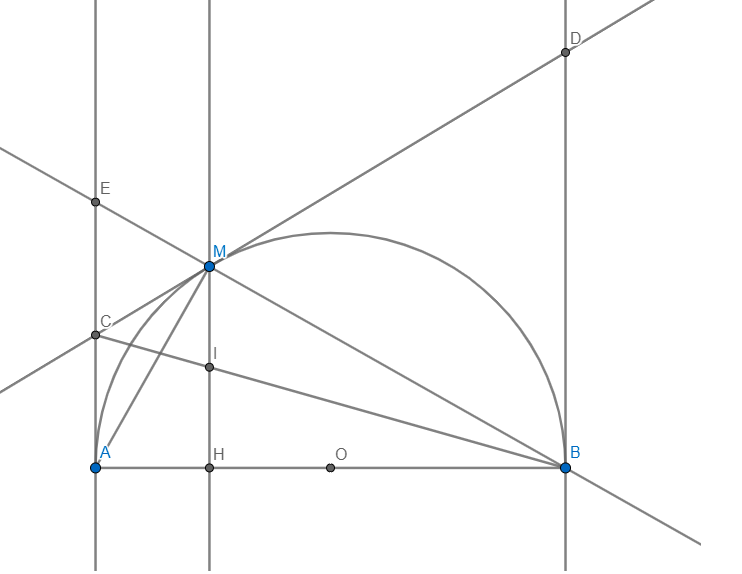
a: Xét ΔMAO và ΔMCO có
MA=MC
AO=CO
MO chung
=>ΔMAO=ΔMCO
=>góc MCO=90 độ
góc MAO+góc MCO=180 độ
=>MAOC nội tiếp đường tròn đường kính MO
=>I là trung điểm của MO
b: góc MCO=90 độ
=>MC là tiếp tuyến của (O)
Xét ΔMCD và ΔMBC có
góc MCD=góc MBC
góc CMD chung
=>ΔMCD đồng dạng với ΔMBC
=>MC/MB=MD/MC
=>MC^2=MB*MD

c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm

a) Tứ giác EFMK có góc E và góc M vuông (vì đều bằng các góc chắn nửa đường tròn) nên là tứ giác nội tiếp.
b) Ta có
(Góc tạo bởi tia tiếp tuyến và dây cung bằng góc nội tiếp cùng chắn cung);
( góc nội tiếp cùng chắn cung )
mà ( là tia phân giác góc IAM)
nên , hay BE là tia phân giác góc ABM.
Mặt khác BE cũng là đường cao trong tam giác ABF nên tam giác ABF cân tại B.
c) Tam giác HAK có AE vừa là phân giác vừa là đường cao nên nó cân tại A. Suy ra E là trung điểm HK.
Tứ giác HFKA có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường nên là hình thoi.
d) HFKA là hình thoi nên FK // HA, suy ra tứ giác IFKA là hình thang.
Để IFKA nội tiếp được đường tròn thì nó phải là hình thang cân, hay tam giác MIA vuông cân tại M.
Khi đó, tam giác MAB vuông cân tại M. Do đó M là điểm chính giữa cung nửa đường tròn AB.