Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

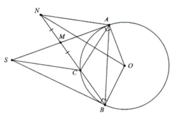
a, S A O ^ + S B O ^ = 90 0 + 90 0 = 180 0
Tứ giác OASB nội tiếp
b, M A C ^ = C B A ^ = 1 2 s đ C A ⏜
=> ∆MAC:∆MBA(g.g)
Từ đó suy ra M A 2 = M B . M C
c, Có M A 2 = M B . M C mà MA = MS => S M M S = M C M S
Chứng minh được ∆MSB:∆MCS
=>
M
B
S
^
=
C
S
M
^
hay
M
B
S
^
=
C
S
A
^
d, Chứng minh
N
A
S
^
=
M
B
S
^
(Vì cùng =
C
S
A
^
)
=> Tứ giác NAOB là từ giác nội tiếp
Chứng minh được A N O ^ = O N B ^
=> ĐPCM

\(a.\Delta MAD\&\Delta MBA:\widehat{MAD}=\widehat{MBA}\left(=\frac{1}{2}\widebat{AD}\right);\widehat{AMB}=\widehat{AMD}\Rightarrow\Delta MAD~\Delta MBA\left(g.g\right)\Rightarrow MD^2=MB.MC\)b.Do I là trung điểm dây CD nên OI vuông góc CD mà ^SBO=90=>S;B;O;I cùng thuộc một đtròn
Mà dễ thấy S;B;A;O cùng thuộc một đtròn nên S;B;I;O;A cùng thuộc một đtròn
Do đó ^SIA=^SBA,^SIB=^SAB.Mà ^SAB=^SBA(do SA,SB là tiếp tuyến (O))=>^SIA=^SIB=>Đpcm
c.^DIE=^DCA=^DBE=>B;D;E;I cùng thuộc một đtròn=>^DEB=^DIB=^SAB=>DE//SA=>DE//BC
d.