Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

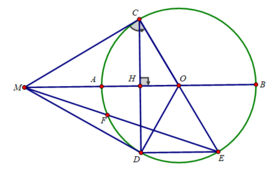
a) Xét tam giác COD cân tại O có OH là đường cao
⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)
Xét ΔMCO và ΔMOD có:
CO = OD
∠(COM) = ∠(MOD)
MO là cạnh chung
⇒ ΔMCO = ΔMOD (c.g.c)
⇒ ∠(MCO) = ∠(MDO)
∠(MCO) = 90 0 nên ∠(MDO) = 90 0
⇒ MD là tiếp tuyến của (O)

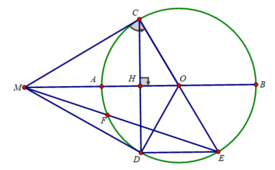
c) Ta có: ΔCOD cân tại O có OH là đường cao cũng là đường trung tuyến của tam giác
⇒ CH = HD = CD/2 ⇒ C H 2 = D H 2 = C D 2 / 4
Tam giác ACH vuông tại H có:
A H 2 + C H 2 = C A 2 ⇒ A H 2 + C D 2 / 4 = C A 2 (1)
Tam giác CHB vuông tại H có:
B H 2 + C H 2 = C B 2 ⇒ B H 2 + C D 2 / 4 = C B 2 (2)
Từ (1) và (2) ta có:
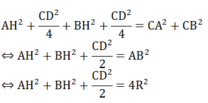

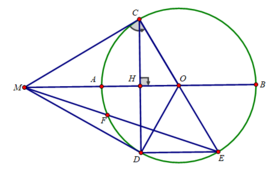
b) Ta có: OM = OA + AM = R + R = 2R
Xét tam giác MCO vuông tại C, CH là đường cao có:
MO 2 = MC 2 + OC 2
![]()
CH.OM = CM.CO
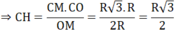
Lại có: CD = 2CH ⇒ CD = R 3
Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D
Theo định lí Py ta go ta có:
CE 2 = CD 2 + DE 2
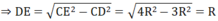

a) Xét ΔOCB có OB=OC(=R)
nên ΔOCB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOCB cân tại O(cmt)
mà OE là đường trung tuyến ứng với cạnh BC(E là trung điểm của BC)
nên OE là đường cao ứng với cạnh BC(Định lí tam giác cân)
⇔OE⊥BC tại E
Xét tứ giác CMOE có
\(\widehat{CMO}\) và \(\widehat{CEO}\) là hai góc đối
\(\widehat{CMO}+\widehat{CEO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: CMOE là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Bạn xem lại đề, sao lại có 2 điểm M trong hình vậy bạn?
d) Ta có: ∠(CFE) = 90 0 (F thuộc đường tròn đường kính CE)
Lại có CF là đường cao nên MC 2 = MF.ME
Tương tự, ta có: MC 2 = MH.MO
⇒ ME.MF = MH.MO
⇒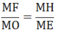
Xét ΔMOF và ΔMEN có:
∠(FMO) chung
⇒ ΔMOF ∼ ΔMEN (c.g.c)
⇒ ∠(MOF) = ∠(MEH)