Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. ta có OM vuông góc CD (OA vuông góc CD:gt)
M là trung điểm CD (bán kính vuông góc dây cung tại trung điểm dây cung)
M là trung điểm OA
=> tứ giác ACOD có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành
mà OC = OD (bán kính)
=> hình bình hành ACOD có hai cạnh kề bằng nhau là hình thoi
b. ta có: BM = OB + OM = OB + 1/2OA = OB +1/2OB = 3/2OB
OB = 2/3 OM
mà BM là trung tuyến của tam giác BCD
=> O là trọng tâm tam giác BCD
mà O cũng là tâm đường tròn ngoại tiếp tam giác BCD
=> tam giác BCD có trọng tâm cũng là tâm đường tròn ngoại tiếp tam giác là tam giác đều

1: Xét \(\left(O\right)\) có
OA là một phần đường kính
CD là dây
OA\(\perp\)CD tại H
Do đó: H là trung điểm của CD
Xét tứ giác OCAD có
H là trung điểm của đường chéo CD
H là trung điểm của đường chéo OA
Do đó: OCAD là hình bình hành
mà OC=OD
nên OCAD là hình thoi
2: Ta có: OCAD là hình thoi
nên OC=OD=AC=AD
mà OA=OC
nên OC=OD=AC=AD=OA
Xét ΔOAC có OA=OC=AC
nên ΔOAC đều

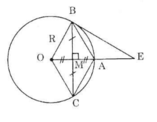
Bán kính OA vuông góc với BC nên MB = MC.
Lại có MO = MA (gt).
Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.
Lại có: OA ⊥ BC nên OBAC là hình thoi.
tứ giác ABCD là hình thoi
tam giác BCD là tam giác cân