Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 :
Xét ΔCHO vuông tại H , có : cos COH = \(\dfrac{OH}{OC }\)( tỉ số lượng giác )
⇔ cos COH = \(\dfrac{R/2}{R}\)=\(\dfrac{1}{2}\)=> \(\widehat{COH }\) = 60 độ
=> \(\widehat{BC }\) = \(\widehat{COH }\) = 60 độ
C/m tương tự => \(\widehat{BD }\) = 60 độ . Ta có \(\widehat{BC }\) + \(\widehat{BD }\) = 60 + 60 = 120 độ
còn lại bạn tự làm nốt nhá

a, Chú ý: K M B ^ = 90 0 và K E B ^ = 90 0 => ĐPCM
b, ∆ABE:∆AKM (g.g)
=> A E A M = A B A K
=> AE.AK = AB.AM = 3 R 2 không đổi
c, ∆OBC đều
=> B O C ⏜ = 60 0 => S = πR 2 6

| a) | góc BEA= 90 ( nội tiếp chắn nửa....), KMB=90 độ (gt). Tứ giác MEBK có 2 góc 2 và M bằng nhau, kề nhau cùng nhìn cạnh KB nên có đpcm |
| b | tam giác KAM đồng dạng BAE ( g.g) ==> AK.AE= AM.AB= 2R. 3R/2= 3R2 |
| c | tam giác OBC đều ( OB=OC=BC ) có BOC =60 độ. S quạt tròn OBC= π. R2. 60/360 |

a) Xét ΔOAB có OA=OB=AB(=R)
nên ΔOAB đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{AOB}=60^0\)
hay \(sđ\stackrel\frown{AB}=60^0\)
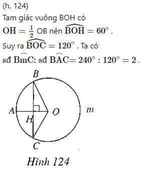
Chứng minh được ∆BOC và ∆BOD là tam giác đều nên suy ra được sđ cung nhỏ C D ⏜ = 120 0 và sđ cung lớn C D ⏜ = 240 0