Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
Ta có :
\(\frac{ab}{a+b}=\frac{bc}{b+c}=\frac{ca}{c+a}\)
\(\Rightarrow\frac{a+b}{ab}=\frac{b+c}{bc}=\frac{c+a}{ca}\)
\(\Rightarrow\frac{1}{b}+\frac{1}{a}=\frac{1}{c}+\frac{1}{b}=\frac{1}{c}+\frac{1}{a}\)
\(\Rightarrow\hept{\begin{cases}\frac{1}{b}+\frac{1}{a}=\frac{1}{c}+\frac{1}{b}\\\frac{1}{c}+\frac{1}{b}=\frac{1}{c}+\frac{1}{a}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\frac{1}{a}=\frac{1}{c}\\\frac{1}{b}=\frac{1}{a}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a=c\\a=b\end{cases}}\)
\(\Rightarrow a=b=c\)
\(\Rightarrow P=\frac{20a^2+4a^2+2020a^2}{a^2+a^2+a^2}=\frac{2044a^2}{3a^2}=\frac{2044}{3}\)

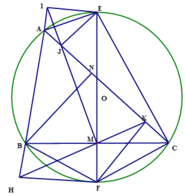
a) Ta có: A I E ^ = A J E ^ = 90 0 nên tứ giác AIEJ nội tiếp.
E M C ^ = E J C ^ = 90 0 nên tứ giác CMJE nội tiếp.
Xét tam giác Δ A E C v à Δ I E M , có
A C E ⏜ = E M I ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác CMJE).
E A C ⏜ = E I M ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác AIEJ).
Do đó hai tam giác Δ A E C ~ Δ I E M đồng dạng
⇒ A E E I = E C E M ⇒ E A . E M = E C . E I (đpcm)


c)
K ẻ B N ⊥ A C N ∈ A C . B A C ⏜ = 60 0 ⇒ A B N ⏜ = 30 0 ⇒ A N = A B 2 = c 2 ⇒ B N 2 = A B 2 − A N 2 = 3 c 2 4 ⇒ B C 2 = B N 2 + C N 2 = 3 c 2 4 + b − c 2 2 = b 2 + c 2 − b c ⇒ B C = b 2 + c 2 − b c
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. Xét tam giác đều BCE có R = O E = 2 3 E M = 2 B C 3 3.2 = 1 3 . 3 b 2 + c 2 − b c

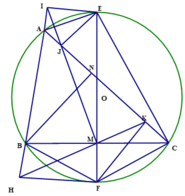
b) Ta có I E M ⏜ = A E C ⏜ ⇒ A E I ⏜ = C E M ⏜ .
Mặt khác A E I ⏜ = A J I ⏜ ( cùng chắn cung IJ), C E M ⏜ = C J M ⏜ ( cùng chắn cung CM). Suy ra C J M ⏜ = A J I ⏜ . Mà I, M nằm hai phía của đường thẳng AC nên C J M ⏜ = A J I ⏜ đối đỉnh suy ra I, J, M thẳng hàng.
Tương tự, ta chứng minh được H, M, K thẳng hàng.
Do tứ giác CFMK nội tiếp nên C F K ⏜ = C M K ⏜ .
Do tứ giác CMJE nội tiếp nên J M E ⏜ = J C E ⏜ .
Mặt khác E C F ⏜ = 90 0 ⇒ C F K ⏜ = J C E ⏜ ( vì cùng phụ với A C F ⏜ ).
Do đó C M K ⏜ = J M E ⏜ ⇒ J M K ⏜ = E M C ⏜ = 90 0 hay I J ⊥ H K

1) Hình vẽ câu 1) đúng
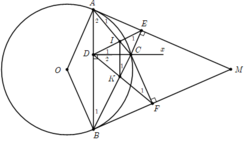
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

Em kham khảo link này nhé.
Câu hỏi của Trần Đức Thắng - Toán lớp 9 - Học toán với OnlineMath
a) có 2 góc vg cùng nhìn 1 cạnh
b)EAC=ACO
tam giác AOC cân tại O
=>.......................
c) theo câu a =>AFE=ADE
từ câu b =>CAB=CAE
CAB=BCD
=>...........................
d) đang suy nghĩ