Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
Do đó: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB là tiếp tuyến của (O)
b: Xét (O) có
ΔBAD nôi tiếp
BD là đường kính
Do đó:ΔBAD vuông tại A
=>AD vuông góc với BA
=>AD//CB


a) Gọi H là giao điểm của OC và AB.
Vì OH ⊥ AB nên HA=HB, suy ra OC là đường trung trực của AB, do đó CB=CA.
Δ CBO = Δ CAO (c.c.c)
⇒ ∠CBO = ∠CAO.
Vì AC là tiếp tuyến của đường trong (O) nên AC ⊥ OA ⇒ ∠CAO = 900.
Do đó ∠CBO= 900.
Vậy CB là tiếp tuyến của đường tròn (O).
b) Xét tam giác HOA vuông tại H, có
OH2= OA2 – AH2 = 152 – 122 = 81 ⇒ OH = 9(cm),
Xét tam giác BOC vuông tại B, có
OB2 = OC.OH ⇒ OC = OB2/OH = 225/9 = 25(cm)
Nhận xét. Ở câu a) ta đã dùng dấu hiệu nhận biết tiếp tuyến để chứng minh CB là tiếp tuyến của đường tròn (O). Ta cũng có thể dựa vào tính chất đối xứng của đường kính để chứng minh CB là tiếp tuyến. Thực vậy B và A đối xứng qua đường thẳng chứa đường kính CO, mà CA là tiếp tuyến nên CB phải là tiếp tuyến.

a) Ta thấy OC là trung trực của AB nên ΔOAC = ΔOBC (c.c.c), duy ra góc OBC vuông. Do đó CB là tiếp tuyến của đường tròn.
b) AI = AB : 2 = 12 cm.
Tính được OI = 9 cm.
cm.

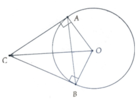
a, ∆OAC = ∆OBC (c.g.c)
=> O B C ^ - O A B ^ = 90 0
=> đpcm
b, Sử dụng hệ thức lượng trong tam giác vuông OBC tính được OC=25cm

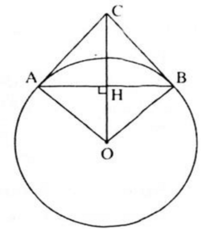
a) Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:
![]()

Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)
⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)
b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)

Vậy OC = 25 cm

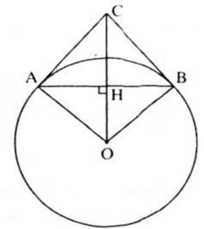
Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)

Vậy OC = 25 cm

a) Xét ΔOAB có OA=OB(=R)
nên ΔOAB cân tại O(Định nghĩa tam giác cân)
Ta có: ΔOAB cân tại O(cmt)
mà OC là đường cao ứng với cạnh đáy AB(OH⊥AB, C∈OH)
nên OC là đường phân giác ứng với cạnh AB(Định lí tam giác cân)
⇒\(\widehat{AOC}=\widehat{BOC}\)
Xét ΔAOC và ΔBOC có
OA=OB(=R)
\(\widehat{AOC}=\widehat{BOC}\)(cmt)
OC chung
Do đó: ΔAOC=ΔBOC(c-g-c)
⇒\(\widehat{OAC}=\widehat{OBC}\)(hai góc tương ứng)
mà \(\widehat{OAC}=90^0\)(CA là tiếp tuyến của (O) có A là tiếp điểm)
nên \(\widehat{OBC}=90^0\)
hay CB⊥OB tại B
Xét (O) có
OB là bán kính
CB⊥OB tại B(cmt)
Do đó: CB là tiếp tuyến của (O)(Dấu hiệu nhận biết tiếp tuyến đường tròn)
b) Xét (O) có
OH là một phần đường kính
AB là dây
OH⊥AB tại H(gt)
Do đó: H là trung điểm của AB(Định lí đường kính vuông góc với dây)
⇒\(BH=\dfrac{AB}{2}=\dfrac{24}{2}=12cm\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔOBC vuông tại B có BH là đường cao ứng với cạnh huyền OC, ta được:
\(\dfrac{1}{BH^2}=\dfrac{1}{BC^2}+\dfrac{1}{BO^2}\)
\(\Leftrightarrow\dfrac{1}{12^2}=\dfrac{1}{BC^2}+\dfrac{1}{20^2}\)
\(\Leftrightarrow\dfrac{1}{BC^2}=\dfrac{1}{12^2}-\dfrac{1}{20^2}=\dfrac{1}{144}-\dfrac{1}{400}=\dfrac{1}{225}\)
\(\Leftrightarrow BC^2=225\)
hay BC=15(cm)
Áp dụng định lí Pytago vào ΔOBC vuông tại B, ta được:
\(OC^2=OB^2+BC^2\)
\(\Leftrightarrow OC^2=15^2+20^2=625\)
hay OC=25(cm)
Vậy: OC=25cm
Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C.
a) Chứng minh rằng CB là tiếp tuyến của đường tòn.
b) Cho bán kính của đường tròn bằng 15cm, AB=24cm. Tính độ dài OC.
Toán lớp 9
ai tích mình tích lại nha
a) Gọi H là giao điểm của OC và AB.
Vì \(OH\) VUÔNG GÓC \(AB\) nên HA=HB, suy ra OC là đường trung trực của AB, do đó CB=CA.
\(\Delta CBO=\Delta CAO\) (c.c.c) .\(\Leftrightarrow\) \(CBO=CAO\)
Vì AC là tiếp tuyến của đường trong (O) nên \(AC\) VUÔNG GÓC \(OA\Leftrightarrow CAO=90\).
Do đó CBO =90 .
Vậy CB là tiếp tuyến của đường tròn (O).
b) Xét tam giác HOA vuông tại H, có
OH\(^2\)=OA\(^2\)-AH\(^2\)=15^2-12^2=81\(\Rightarrow\)OH=9(cm)
Xét tam giác BOC vuông tại B, có OB^2=OC.OH sUY RA OC=OB^2/OH=225/9=25(CM)
Nhận xét. Ở câu a) ta đã dùng dấu hiệu nhận biết tiếp tuyến để chứng minh CB là tiếp tuyến của đường tròn (O). Ta cũng có thể dựa vào tính chất đối xứng của đường kính để chứng minh CB là tiếp tuyến. Thực vậy B và A đối xứng qua đường thẳng chứa đường kính CO, mà CA là tiếp tuyến nên CB phải là tiếp tuyến.