Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Hình vẽ:
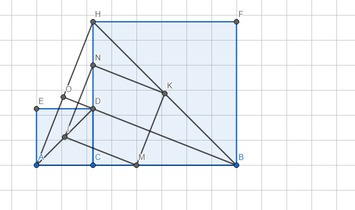
a) -Xét △ACH và △DCB có:
\(AC=DC\) (ACDE là hình vuông).
\(HC=CB\) (BCHF là hình vuông).
\(\widehat{ACH}=\widehat{DCB}=90^0\).
=>△ACH=△DCB (c-g-c).
=>\(AH=BD\) (2 cạnh tương ứng).
*BD cắt AH tại O.
- Ta có: \(\widehat{AHC}=\widehat{DBC}\) (△ACH=△DCB).
Mà \(\widehat{DBC}+\widehat{BDC}=90^0\) (△DCB vuông tại C).
=>\(\widehat{AHC}+\widehat{BDC}=90^0\).
Mà \(\widehat{BDC}=\widehat{ODH}\) (đối đỉnh).
=>\(\widehat{AHC}+\widehat{ODH}=90^0\).
Mà \(\widehat{AHC}+\widehat{ODH}+\widehat{HOD}=180^0\) (tổng 3 góc trong △HOD).
=>\(90^0+\widehat{HOD}=180^0\).
=>\(\widehat{HOD}=90^0\) nên \(AH\perp BD\) tại O.
b) - Xét △ADH có:
I là trung điểm AD (I là tâm đối xứng của hình vuông ACDE).
N là trung điểm DH (gt).
=>IN là đường trung bình của △ADH.
=>IN=\(\dfrac{1}{2}AH\) (1) ; IN//AH
- Xét △ADB có:
I là trung điểm AD (I là tâm đối xứng của hình vuông ACDE).
M là trung điểm AB (gt).
=>IM là đường trung bình của △ADB.
=>IM=\(\dfrac{1}{2}BD\)=\(\dfrac{1}{2}AH\). (2); IM//BD.
- Từ (1) và (2) suy ra: \(IM=IN\)
- Ta có: \(AH\perp BD\) (cmt) ; IN//AH (cmt) ; IM//BD(cmt).
=>\(IN\perp IN\) tại I.
- Xét △DHB có:
K là trung điểm BH (K là tâm đối xứng của hình vuông BCHF).
N là trung điểm DH (gt).
=>KN là đường trung bình của △DHB.
=>KN=\(\dfrac{1}{2}BD\) (3) ; NK//BD.
- Từ (3) và (4) suy ra: KN=IM mà KN//IM//BD.
=>NKMI là hình bình hành mà IM=IN (cmt)
=>NKMI là hình thoi mà \(\widehat{NIM}=90^0\) (\(IM\perp IN\) tại I).
=>NKMI là hình vuông.

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD