Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
b: ΔAHB vuông tại H có HD là đường cao
nên AD*AB=AH^2
ΔAHC vuông tại H có HE là đường cao
nên AE*AC=AH^2=AD*AB
=>AE/AB=AD/AC
=>ΔAED đồng dạng với ΔABC
c: ΔAED đồng dạng với ΔABC
=>\(\dfrac{S_{AED}}{S_{ABC}}=\left(\dfrac{ED}{BC}\right)^2=\dfrac{4}{25}\)
=>\(S_{AED}=\dfrac{4}{25}\cdot80=\dfrac{320}{25}=12.8\left(cm^2\right)\)

\(\widehat{BHD}=\widehat{HAB}\)
\(\widehat{HAB}=\widehat{ADE}\)
Do đó: \(\widehat{ADE}=\widehat{BHD}\)

a: Xét ΔHCA vuông tại H và ΔACB vuông tại A có
góc HCA chung
Do đó:ΔHCA\(\sim\)ΔACB
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(BH\cdot BC=AB^2\)
c: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
XétΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

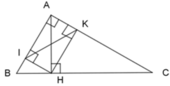
Gọi I, K lần lượt là hình chiếu của H lên AB và AC.
⇒ H I A ^ = H K A ^ = 90 ∘
Xét tứ giác AIHK có: I A K ^ = H I A ^ = H K A ^ = 90 ∘
=> Tứ giác AIHK là hình chữ nhật (dhnb)
+) Xét ΔAIK và ΔIAH ta có:
AI chung
AK = IH (theo tính chất của hình chữ nhật)
AH = IK (theo tính chất của hình chữ nhật)
=> ΔAIK = ΔIAH (c - c - c) (1)
Xét 2 tam giác vuông ΔIAH và ΔHAB có: A chung
=> ΔIAH ~ ΔHAB (g - g) (2)
Xét 2 tam giác vuông ΔHAB và ΔACB có: B chung
=> ΔHAB ~ ΔACB (g - g) (3)
Từ (1), (2) và (3) ta có: ΔAIK ~ ΔACB
Đáp án: A

a, Xét tứ giác ADHE có :
^A = ^ADH = ^HEA = 900
Vậy tứ giác ADHE là hcn
Vậy AH = DE ( 2 đường chéo bằng nhau )
b, Xét tam giác AEH và tam giác AHC có :
^AEH = ^AHC = 900
^A _ chung
Vậy tam giác AEH ~ tam giác AHC ( g.g )
=> AH/AC = AE/AH => AH^2 = AE.AC (1)
tương tự với tam giác ADH ~ tam giác AHB (g.g)
=> AD/AH = AH/AB => AH^2=AD.AB (2)
Từ (1) ; (2) suy ra AE.AC = AD.AB
c, Xét tam giác ABH và tam giác CAH
^AHB = ^CHA = 900
^ABH = ^CAH ( cùng phụ ^BAH )
Vậy tam giác ABH ~ tam giác CAH (g.g)
=> AH/CH = BH/AH => AH^2 = BH.CH
=> CH = AH^2/BH = 144/9 = 16
=> BC = BH + CH = 25 cm
Diện tích tam giác ABC là : SABC = 1/2 . AH . BC
= 1/2 . 12 . 25 = 150 cm2

a: BC=35cm
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{3}=\dfrac{CD}{4}=\dfrac{BD+CD}{3+4}=\dfrac{35}{7}=5\)
Do đó:BD=15cm; CD=20cm
b: Xét ΔABC có DE//AB
nên DE/AB=CD/BC
=>DE/21=20/35=4/7
=>DE=12cm
Xét ΔABC cso DE//BC
nên CE/CA=ED/AB
=>CE/28=12/21=4/7
=>CE=12cm
e tự vẽ hình nha
a) vì tg ABC vg tại A(gt)
\(\Rightarrow AB^2+AC^2=BC^2\left(pytago\right)\\ \Leftrightarrow28^2+21^2=BC^2\\ \Leftrightarrow BC=35\left(cm\right)\)
có AD là pgiac(gt)
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{21}{28}\\ \Leftrightarrow\dfrac{BD}{21}=\dfrac{CD}{28}=\dfrac{BD+CD}{21+28}=\dfrac{BC}{49}=\dfrac{35}{49}\)
\(+\dfrac{BD}{21}=\dfrac{35}{49}\Rightarrow BD=15\left(cm\right)\\ +\dfrac{CD}{28}=\dfrac{35}{49}\Rightarrow CD=20\left(cm\right)\)
b) xét tgiac ABC và tgac EDC có:
+ góc C chung
+ góc E = góc A (=90 độ)
+ góc D = góc B ( sltrong, DE//AB vì cùng vg góc AC)
\(\Rightarrow\Delta ABC\sim\Delta EDC\left(ggg\right)\\ \Rightarrow\dfrac{CB}{CD}=\dfrac{AB}{ED}=\dfrac{AC}{EC}\)
\(\Leftrightarrow\dfrac{35}{20}=\dfrac{AB}{ED}=\dfrac{AC}{EC}\)
\(+ED=\dfrac{20.21}{35}=12\left(cm\right)\\ +EC=\dfrac{28.20}{35}=16\left(cm\right)\)
c) ở trên câu b a làm có luôn tam giác với tỉ số r đấy e chép xuống
