Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

PTHĐGĐ của (C) với (d) :
(
ko là nghiệm)
Viết lại: (*).Theo Viet có:
Ta có: nên (C) với (d) luôn cắt nhau tại 2 điểm phân biệt
là giao điểm của (C) với (d)
Theo giả thiết: . Đạt giá trị nhỏ nhất khi
Giải thằng này thu được:

Đáp án C
Đồ thị hàm số y = x 3 - 3 x + 1 là đồ thị bên dưới
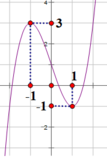
Từ đồ thị hàm số y = x 3 - 3 x + 1 suy ra đồ thị hàm số y = x 3 - 3 x + 1 là đồ thị bên dưới
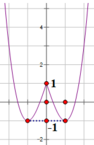
Dựa vào đồ thị hàm số y = x 3 - 3 x + 1 và đồ thị hàm số y = 2 m - 1
Ta có: đường thẳng y = 2 m - 1 cắt đồ thị hàm số y = x 3 - 3 x + 1 tại 4 điểm phân biệt
⇔ - 1 < 2 m - 1 < 1 ⇔ 0 < m < 1

Phương trình hoành độ giao điểm: \(x^4-5x^2-m+4=0\)
Đặt \(x^2=t\Rightarrow t^2-5t-m+4=0\) (1)
Gọi 4 hoành độ giao điểm là \(x_1< x_2< x_3< x_4\) và \(t_1< t_2\) là 2 nghiệm dương phân biệt của (1) thì: \(\left\{{}\begin{matrix}x_1=-\sqrt{t_2}\\x_2=-\sqrt{t_1}\\x_3=\sqrt{t_1}\\x_4=-\sqrt{t_2}\end{matrix}\right.\)
Do 4 điểm cách đều \(\Rightarrow x_2-x_1=x_3-x_2\Rightarrow x_1+x_3=2x_2\)
\(\Rightarrow-\sqrt{t_2}+\sqrt{t_1}=-2\sqrt{t_1}\) \(\Rightarrow3\sqrt{t_1}=\sqrt{t_2}\Rightarrow t_2=9t_1\)
\(\Rightarrow\left\{{}\begin{matrix}t_1+t_2=5\\t_2=9t_1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}t_1=\dfrac{1}{2}\\t_2=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow-m+4=t_1t_2=\dfrac{9}{4}\)
\(\Rightarrow m=\dfrac{7}{4}\)

Lời giải:
PT hoành độ giao điểm:
\(x^3-2(m+1)x^2+(5m+1)x-2m-2=0\)
\(\Leftrightarrow (x-2)(x^2-2mx+m+1)=0\)
Vì \(A(2,0)\) nên hoành độ hai điểm \(B,C\) sẽ là nghiệm của PT \(x^2-2mx+m+1=0\)
Điều kiện: \(\Delta'=m^2-(m+1)>0\)
Khi đó, áp dụng định lý Viete, nếu $x_1,x_2$ là hai nghiệm của PT thì \(\left\{\begin{matrix} x_1+x_2=2m\\ x_1x_2=m+1\end{matrix}\right.\)
Nhận thấy hai điểm $B,C$ nằm trên $Ox$ mà một điểm nằm trong đường tròn \(x^2+y^2=1\) nên \((x_1-1)(x_2-1)<0\)
\(\Leftrightarrow x_1x_2-(x_1+x_2)+1<0\Leftrightarrow m+1-2m+1<0\)
\(\Leftrightarrow m>2\). Thử lại ta thấy thỏa mãn điều kiện \(\Delta'\)
Vậy \(m>2\)

