Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: u3 = u1.q2 ; u5 = u1.q5.
Theo đề bài, ta có hệ phương trình :
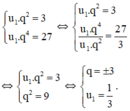
+ Với q = 3 ta có cấp số nhân : 1/3 ; 1 ; 3 ; 9 ; 27.
+ Với q = -3 ta có cấp số nhân : 1/3 ; -1 ; 3 ; -9 ; 27.

\(\left\{{}\begin{matrix}u_{14}=u_1+13d=18\\u_4=u_1+3d=-12\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}d=3\\u_1=-21\end{matrix}\right.\)
Tổng 16 số hạng đầu tiên:
\(S_{16}=\frac{16\left(2u_1+15d\right)}{2}=24\)

Phương pháp:
Số hạng tổng quát của CSN : u n = u 1 . q n - 1
Cách giải:
Ta có: u 1 = 2 , q = 3
![]()
Chọn D

a)
| -1 | 3 | 7 | 11 | 15 | 19 | 23 | 27 |
| 27 | 23 | 19 | 15 | 11 | 7 | 3 | - 1 |
Nhận xét: Tổng của các số hạng ở mỗi cột bằng nhau và bằng 26
b) Tổng các số hạng của cấp số cộng là: 26.8/2 = 104
Đáp án B
Hướng dẫn giải.
Ta có u n = u 1 . q n - 1
⇒ u 5 = - 3 . 2 3 4 = - 16 27