Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, ĐKXĐ: \(x\ne1;x\ne-1\)
b, Với \(x\ne1;x\ne-1\)
\(B=\left[\dfrac{x+1}{2\left(x-1\right)}+\dfrac{3}{\left(x-1\right)\left(x+1\right)}-\dfrac{x+3}{2\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\left[\dfrac{x^2+2x+1+6-x^2-2x+3}{2\left(x-1\right)\left(x+1\right)}\right]\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =\dfrac{5}{x^2-1}\cdot\dfrac{4\left(x^2-1\right)}{5}\\ =4\)
=> ĐPCM

a, ĐKXĐ: x2-4≠0 ⇔ x≠±2
b, \(\dfrac{x^2-4x+4}{x^2-4}\)=\(\dfrac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\)=\(\dfrac{x-2}{x+2}\)
c, |x|=3
TH1: x≥0 thì x=3 (TMĐK)
TH1: x<0 thì x=-3 (TMĐK)
Thay x=3 và biểu thức ta có:
\(\dfrac{3-2}{3+2}\)=\(\dfrac{1}{5}\)
Thay x=-3 và biểu thức ta có:
\(\dfrac{-3-2}{-3+2}\)=5

`a)ĐK:x^2-4 ne 0<=>x^2 ne 4`
`<=>x ne 2,x ne -2`
`b)A=(x^2-4x+4)/(x^2-4)`
`=(x-2)^2/((x-2)(x+2))`
`=(x-2)/(x+2)`
`c)|x|=3`
`<=>` \(\left[ \begin{array}{l}x=3\\x=-3\end{array} \right.\)
`<=>` \(\left[ \begin{array}{l}A=\dfrac{3-2}{3+2}=\dfrac15\\x=\dfrac{-3-2}{-3+2}=5\end{array} \right.\)
`d)A=2`
`=>x-2=2(x+2)`
`<=>x-2=2x+4`
`<=>x=-6`
a, ĐKXĐ: \(x^2-4\ne0\Leftrightarrow x\ne\pm2\)
b, Ta có: \(\dfrac{x^2-4x+4}{x^2-4}=\dfrac{\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x-2}{x+2}\) (*)
c, \(\left|x\right|=3\Rightarrow x=\pm3\)
_ Thay x = 3 vào (*), ta được: \(\dfrac{3-2}{3+2}=\dfrac{1}{5}\)
_ Thay x = -3 vào (*), ta được: \(\dfrac{-3-2}{-3+2}=5\)
d, Có: \(\dfrac{x-2}{x+2}=2\)
\(\Leftrightarrow x-2=2\left(x+2\right)\)
\(\Leftrightarrow x-2=2x+4\)
\(\Leftrightarrow x=-6\left(tm\right)\)
Vậy...

Bạn tham khảo nha! Mình không hiểu đề câu d lắm nên không làm câu d, nhưng theo mình đoán câu d có phải sẽ là tìm x để phân thức được giá trị nguyên có đúng không nhỉ?


a) Với điều kiện x ≠ -2 thì giá trị của phân thức xác định
b) \(\dfrac{2x^2-4x+8}{x^3+8}\)
= \(\dfrac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}\)
= \(\dfrac{2}{x+2}\)
c) Thay x = 2 vào phân thức, ta được :
\(\dfrac{2}{2+2}=\dfrac{2}{4}=\dfrac{1}{2}\)
d) Với x ≠ -2 thì giá trị của phân thức được xác định

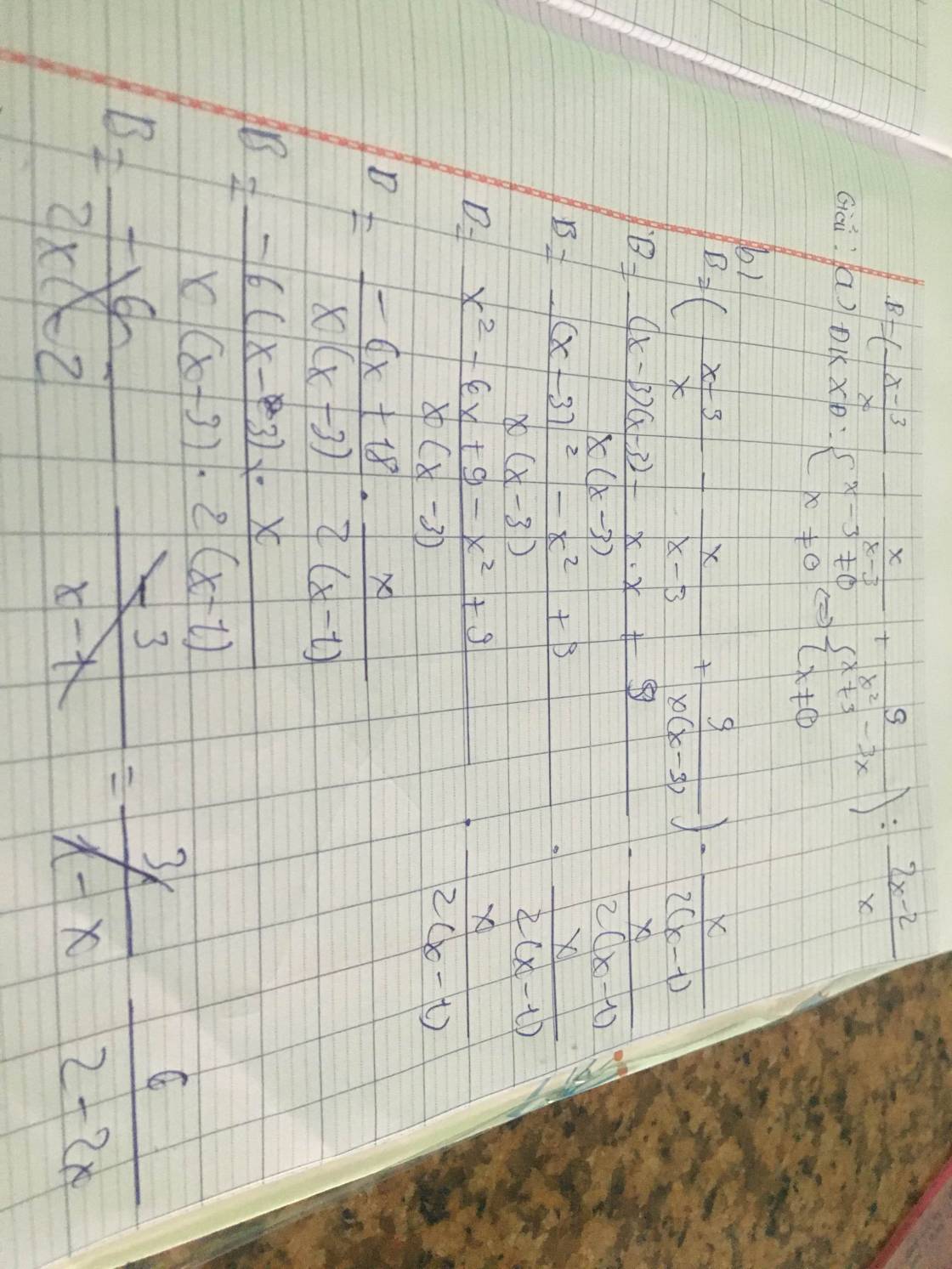 c/
c/
Ta có : B=2=>6/2-2x
<=>6=4-4x
<=>6-4=-4x
<=>-4x=2
<=>x=2/-4=-1/2
d/ĐKXĐ:2-2x≠0
<=>2(1-x)≠0<=>-2(x-1)≠0
<=>x≠1
Để giá trị của biểu thức B nguyên thì 2-2x là Ư(6)
=>2-2x ∈ Ư(6)={±1;±2;±3;±6) Nếu 2-2x=1=> -2x=-1=>x=1/2( thoả mãng)
Rồi còn nhiêu bạn tự xét trường hợp y trang cách làm ở trênn nnhan :;)).À sẽ có mấy cái trường hợp nó giống ĐKXĐ thì bạn ghi trong ngoặc ko thoã mãn nhan.

a, ĐKXĐ: x3+8≠0 ⇔ x≠-2
b, \(\dfrac{2x^2-4x+8}{x^3+8}\)=\(\dfrac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}\)=\(\dfrac{2}{x+2}\)
c, vì x=2 thỏa mãn đkxđ nên khi thay vào biểu thức ta có:
\(\dfrac{2}{2+2}\)=\(\dfrac{1}{2}\)
d, \(\dfrac{2}{x+2}\)=2 ⇔ 2x+4=2 ⇔ 2x=-2 ⇔ x=-1 (TMĐKXĐ)
Nên khi phân thức bằng 2 thì x=-1

\(a,ĐK:x\ne3;x\ne-2\\ b,A=\dfrac{\left(x-3\right)^2}{\left(x-3\right)\left(x+2\right)}=\dfrac{x-3}{x+2}\\ c,A\in Z\Leftrightarrow\dfrac{x+2-5}{x+2}=1-\dfrac{5}{x+2}\in Z\\ \Leftrightarrow x+2\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow x\in\left\{-7;-3;-1;3\right\}\left(tm\right)\)
a) C được xác định <=> x khác +- 2
b) Ta có : \(C=\dfrac{x^3}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}-\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^3-x^2-2x-2x+4}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2\left(x-1\right)-4\left(x-1\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{\left(x-1\right)\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=x-1\)
Để C = 0 thì x - 1 = 0 <=> x = 1 (tm)
c) Để C nhận giá trị dương thì x - 1 > 0 <=> x > 1
Kết hợp với ĐK => Với x > 1 và x khác 2 thì C nhận giá trị dương
mình cảm ơn ạ