Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
B=\(\frac{4^2-2^2}{2^2\times4^2}+\frac{6^2-4^2}{4^2\times6^2}+...+\frac{98^2-96^2}{96^2\times98^2}+\frac{100^2-98^2}{98^2\times100^2}\)
=\(\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-\frac{1}{6^2}+...+\frac{1}{96^2}-\frac{1}{98^2}+\frac{1}{98^2}-\frac{1}{100^2}\)
= \(\frac{1}{4}-\frac{1}{100^2}< \frac{1}{4}\)

\(B=\frac{12}{\left(2.4\right)^2}+\frac{20}{\left(4.6\right)^2}+............+\frac{388}{\left(96.98\right)^2}+\frac{396}{\left(98.100\right)^2}\)
\(B=\frac{4^2-2^2}{\left(2.4\right)^2}+\frac{6^2-4^2}{\left(4.6\right)^2}+..........+\frac{98^2-96^2}{\left(96.98\right)^2}+\frac{100^2-98^2}{\left(98.100\right)^2}\)
\(B=\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-...............-\frac{1}{98^2}+\frac{1}{98^2}-\frac{1}{100^2}\)
\(B=\frac{1}{2^2}-\frac{1}{100^2}\)
\(B=\frac{1}{4}-\frac{1}{10000}\)
\(B=\frac{2500}{10000}-\frac{1}{10000}\)
\(B=\frac{2499}{10000}\)
Vậy B = \(\frac{2499}{10000}\)

Bài 1:
ta có: \(B=\frac{12}{\left(2.4\right)^2}+\frac{20}{\left(4.6\right)^2}+...+\frac{388}{\left(96.98\right)^2}+\frac{396}{\left(98.100\right)^2}\)
\(B=\frac{4^2-2^2}{2^2.4^2}+\frac{6^2-4^2}{4^2.6^2}+...+\frac{98^2-96^2}{96^2.98^2}+\frac{100^2-98^2}{98^2.100^2}\)
\(B=\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-\frac{1}{6^2}+...+\frac{1}{96^2}-\frac{1}{98^2}+\frac{1}{98^2}-\frac{1}{100^2}\)
\(B=\frac{1}{2^2}-\frac{1}{100^2}\)
\(B=\frac{1}{4}-\frac{1}{100^2}< \frac{1}{4}\)
\(\Rightarrow B< \frac{1}{4}\)
Bài 2:
ta có: \(B=\frac{2015+2016+2017}{2016+2017+2018}\)
\(B=\frac{2015}{2016+2017+2018}+\frac{2016}{2016+2017+2018}+\frac{2017}{2016+2017+2018}\)
mà \(\frac{2015}{2016}>\frac{2015}{2016+2017+2018}\)
\(\frac{2016}{2017}>\frac{2016}{2016+2017+2018}\)
\(\frac{2017}{2018}>\frac{2017}{2016+2017+2018}\)
\(\Rightarrow\frac{2015}{2016}+\frac{2016}{2017}+\frac{2017}{2018}>\frac{2015}{2016+2017+2018}+\frac{2016}{2016+2017+2018}+\frac{2017}{2016+2017+2018}\)
\(\Rightarrow A>B\)
Học tốt nhé bn !!

B = \(\dfrac{12}{\left(2.4\right)^2}+\dfrac{20}{\left(4.6\right)^2}+...+\dfrac{388}{\left(96.98\right)^2}+\dfrac{396}{\left(98.100\right)^2}\)
= \(\dfrac{4^2-2^2}{2^{2^{ }}.4^{2^{ }}}+\dfrac{6^{2^{ }}-4^2}{4^2.6^2}+...+\dfrac{98^2-96^2}{96^2.98^2}+\dfrac{100^2-98^2}{98^2.100^2}\)
=\(\dfrac{1}{2^{2^{ }}}-\dfrac{1}{4^{2^{ }}}+\dfrac{1}{4^2}-\dfrac{1}{6^2}+\dfrac{1}{6^2}+....-\dfrac{1}{98^2}+\dfrac{1}{98^2}-\dfrac{1}{100^2}\)
= \(\dfrac{1}{2^2}-\dfrac{1}{100^2}=\dfrac{1}{4}-\dfrac{1}{100^2}< \dfrac{1}{4}\)
Vậy B < \(\dfrac{1}{4}\)
B = 12(2.4)2+20(4.6)2+...+388(96.98)2+396(98.100)212(2.4)2+20(4.6)2+...+388(96.98)2+396(98.100)2
= 42−2222.42+62−4242.62+...+982−962962.982+1002−982982.100242−2222.42+62−4242.62+...+982−962962.982+1002−982982.1002
=122−142+142−162+162+....−1982+1982−11002122−142+142−162+162+....−1982+1982−11002
= 122−11002=14−11002<14122−11002=14−11002<14
Vậy B < 14

B=\(\frac{12}{2^2.4^2}+\frac{20}{4^2.6^2}+......+\frac{388}{96^2.98^2}+\frac{396}{98^2.100^2}\)
=\(\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-\frac{1}{6^2}+...+\frac{1}{96^2}-\frac{1}{98^2}+\frac{1}{98^2}-\frac{1}{100^2}\)
=\(\frac{1}{2^2}-\frac{1}{100^2}\)
=\(\frac{2599}{10000}< \frac{2500}{10000}=\frac{1}{4}\)
=> B<\(\frac{1}{4}\)
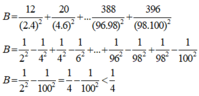
Ta có :
\(B=\frac{12}{\left(2.4\right)^2}+\frac{20}{\left(4.6\right)^2}+...+\frac{388}{\left(96.98\right)^2}+\frac{396}{\left(98.100\right)^2}\)
\(=\frac{12}{4.16}+\frac{20}{16.36}+...+\frac{388}{9216.9604}+\frac{396}{9604.10000}\)
\(=\frac{1}{4}-\frac{1}{16}+\frac{1}{16}-\frac{1}{36}+...+\frac{1}{9604}-\frac{1}{10000}\)
\(=\frac{1}{4}-\frac{1}{10000}< \frac{1}{4}\)
\(\Leftrightarrow B< \frac{1}{4}\)
B=\(\frac{12}{4.16}\)+\(\frac{20}{16.36}\)+...+\(\frac{396}{9604.10000}\)
Ta có:\(\frac{12}{4.16}\)=\(\frac{1}{4}\)-\(\frac{1}{16}\)
\(\frac{20}{16.36}\)=\(\frac{1}{16}\)-\(\frac{1}{36}\)
...
Khi đó:B=\(\frac{1}{4}\)-\(\frac{1}{16}\)+\(\frac{1}{16}\)-\(\frac{1}{36}\)+...+\(\frac{1}{9604}\)-\(\frac{1}{10000}\)=\(\frac{1}{4}\)-\(\frac{1}{10000}\)<\(\frac{1}{4}\)
Vậy: B<\(\frac{1}{4}\)