FH
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BP
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 4 2022
\(M=75.4\left(4^{2020}+4^{2019}+...+4+1\right)+75+25=\)
\(=300.\left(4^{2020}+4^{2019}+...+4+1\right)+100=\)
\(=100\left[3.\left(4^{2020}+4^{2019}+...+4+1\right)+1\right]⋮100\)
NV
1
AH
Akai Haruma
Giáo viên
29 tháng 6 2023
Lời giải:
Xét $A=4^{2021}+4^{2020}+...+4^2+4+1$
$4A=4^{2022}+4^{2021}+...+4^3+4^2+4$
$\Rightarrow 4A-A=4^{2022}-1$
$\Rightarrow 3A=4^{2022}-1$
$\Rightarrow M=75A+25=25(4^{2022}-1)+25=25.4^{2022}=100.4^{2021}\vdots 100$
Ta có đpcm.
12 tháng 5 2022
Đặt \(D=1+4+...+4^{2019}\)
\(\Leftrightarrow4D=4+4^2+...+4^{2020}\)
\(\Leftrightarrow D=\dfrac{4^{2020}-1}{3}\)
\(C=75\cdot D+25\)
\(=25\left(4^{2020}-1\right)+25=25\cdot4\cdot4^{2019}⋮100\)
TT
1
27 tháng 6 2023
B=(3+3^2)+3^2(3+3^2)+...+3^98(3+3^2)
=12(1+3^2+...+3^98) chia hết cho 12
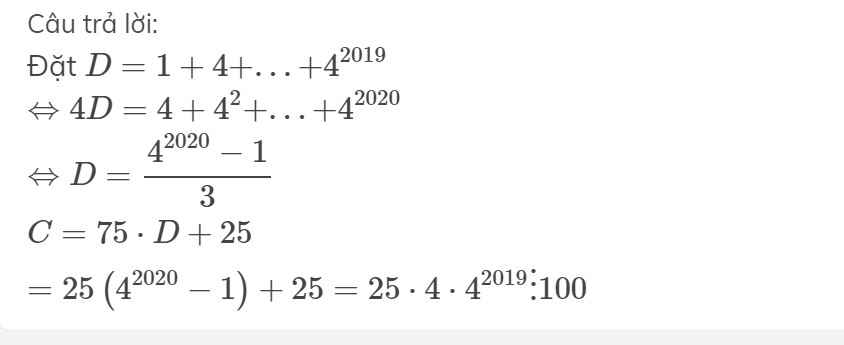
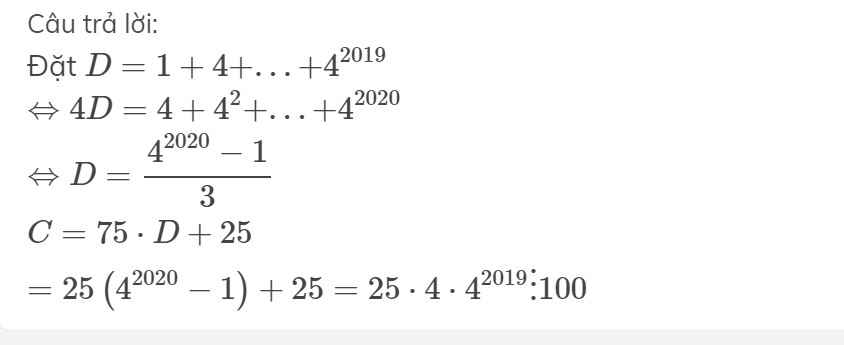
=> B = 75.41993 + 75.41992 + ... + 75.4 + 75 + 25
= 25.3.4.41992 + 25.3.4.41991 + ... + 25.3.4 + 100
= 100.3.41992 + 100.3.41991 + ... + 100.3 + 100
= 100 ( 41992 + 41991 + .... + 3 + 1 ) CHIA HẾT CHO 100
vậy cho mình hỏi Đinh Đức Hùng, số 41993 sẽ sao ạ ?