Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cái bài này thì có lẽ bạn nên chứng minh AM⊥FE là nó ra liền à
Tứ giác AEHF là hình chữ nhật (3 góc vuông) \(\Rightarrow HE=AF\) và \(AE=HF\)
\(S_{ABC}=S_{ABH}+S_{ACH}=\dfrac{1}{2}HE.AB+\dfrac{1}{2}HF.AC=\dfrac{1}{2}AB.AF+\dfrac{1}{2}AC.AE\)
Gọi K là trung điểm AB \(\Rightarrow MK\) là đường trung bình tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}MK=\dfrac{1}{2}AC\\MK\perp AB\end{matrix}\right.\)
Gọi D là trung điểm AC \(\Rightarrow MD\) là đtb tam giác ABC \(\Rightarrow\left\{{}\begin{matrix}MD=\dfrac{1}{2}AB\\MD\perp AC\end{matrix}\right.\)
\(S_{AEMF}=S_{ABC}-\left(S_{BME}+S_{CMF}\right)=S_{ABC}-\left(\dfrac{1}{2}MK.BE+\dfrac{1}{2}MD.CF\right)\)
\(=S_{ABC}-\dfrac{1}{2}\left(\dfrac{1}{2}AC.\left(AB-AE\right)+\dfrac{1}{2}AB.\left(AC-AF\right)\right)\)
\(=S_{ABC}-\dfrac{1}{2}\left(AB.AC-\left(\dfrac{1}{2}AC.AE+\dfrac{1}{2}AB.AF\right)\right)\)
\(=S_{ABC}-\dfrac{1}{2}\left(2S_{ABC}-S_{ABC}\right)=\dfrac{1}{2}S_{ABC}\) (đpcm)

a: Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AC=AD\cdot AB\)
b: Ta có: \(AE\cdot AC=AD\cdot AB\)
nên \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Xét ΔADE và ΔACB có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
\(\widehat{DAE}\) chung
Do đó: ΔADE\(\sim\)ΔACB

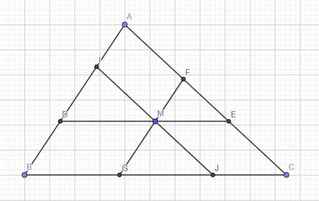
\(\left\{{}\begin{matrix}\widehat{MGJ}=\widehat{B}\left(\text{đồng vị}\right)\\\widehat{MJG}=\widehat{C}\left(\text{đồng vị}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MGJ\sim\Delta ABC\) theo tỉ số \(k_1=\dfrac{GJ}{BC}\)
\(\Rightarrow S_{ABC}.k_1^2=S_{MGJ}\Rightarrow k_1=\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}=\dfrac{GJ}{BC}\) (1)
Tương tự: \(\dfrac{DM}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\), mà BDMG là hbh (2 cặp cạnh đối song song)
\(\Rightarrow DM=BG\Rightarrow\dfrac{BG}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\) (2)
Tương tự: \(\dfrac{CJ}{BC}=\sqrt{\dfrac{S_{FME}}{S_{ABC}}}\) (3)
Cộng vế (1);(2);(3) \(\Rightarrow\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}+\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}+\sqrt{\dfrac{S_{FME}}{S_{ABC}}}=\dfrac{BG+GJ+JC}{BC}=1\)
\(\Rightarrow S_{ABC}=\left(\sqrt{S_{MGJ}}+\sqrt{S_{IDM}}+\sqrt{S_{FME}}\right)^2\le3\left(S_{MGJ}+S_{IDM}+S_{FME}\right)\)
Mà \(S_{MGJ}+S_{IDM}+S_{FME}=S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\)
\(\Rightarrow S_{ABC}\le3\left[S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\right]\)
\(\Rightarrow S_{AIMF}+S_{BGMD}+S_{CEMJ}\le\dfrac{2}{3}S_{ABC}\)

Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông đối với tam giác vuông $AHB$, đường cao $HE$:
$EA.EB=HE^2$
Tương tự: $FA.FC=HF^2$
$\Rightarrow EA.EB+FA.FC=HE^2+HF^2=EF^2(1)$ (định lý Pitago)
Mặt khác: Dễ thấy $HEAF$ là hình chữ nhật do có 3 góc $\widehat{E}=\widehat{A}=\widehat{F}=90^0$
$\Rightarrow EF=HA$
$\Rightarrow EF^2=HA^2(2)$
Áp dụng hệ thức lượng trong tam giác vuông $ABC$:
$AH^2=HB.HC(3)$
Từ $(1);(2); (3)\Rightarrow EA.EB+FA.FC=HB.HC$ (đpcm)
a) Xét tứ giác AEHF có
\(\widehat{FAE}=90^0\)
\(\widehat{AFH}=90^0\)
\(\widehat{AEH}=90^0\)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
Suy ra: AH=EF(hai đường chéo)