Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có thiếu ĐK nào k bạn ?
áp dụng BĐT cauchy :
\(\dfrac{b}{\left(a+\sqrt{b}\right)^2}+\dfrac{d}{\left(c+\sqrt{d}\right)^2}\ge2\sqrt{\dfrac{bd}{\left(a+\sqrt{b}\right)^2\left(c+\sqrt{d}\right)^2}}=\dfrac{2\sqrt{bd}}{\left(a+\sqrt{b}\right)\left(c+\sqrt{d}\right)}\)
việc còn lại cần chứng minh \(\left(a+\sqrt{b}\right)\left(c+\sqrt{d}\right)\le2\left(ac+\sqrt{bd}\right)\)(đúng theo BĐT chebyshev)(không mất tính tổng quát giả sừ \(a\le\sqrt{b};c\le\sqrt{d}\))
dấu = xảy ra khi \(a=\sqrt{b};c=\sqrt{d}\)

Theo tính chất dãy tỉ số bằng nhau, đặt:
\(\dfrac{a}{A}=\dfrac{b}{B}=\dfrac{c}{C}=\dfrac{d}{D}=\dfrac{a+b+c+d}{A+B+C+D}=k>0\)
\(\Rightarrow a=kA;b=kB;c=kC;d=kD;a+b+c+d=k\left(A+B+C+D\right)\)
Do đó:
\(\sqrt{aA}+\sqrt{bB}+\sqrt{cC}+\sqrt{dD}=\sqrt{kA^2}+\sqrt{kB^2}+\sqrt{kC^2}+\sqrt{kD^2}\)
\(=\sqrt{k}\left(A+B+C+D\right)\) (1)
\(\sqrt{\left(a+b+c+d\right)\left(A+B+C+D\right)}=\sqrt{k\left(A+B+C+D\right)^2}=\sqrt{k}\left(A+B+C+D\right)\) (2)
Từ (1);(2) suy ra điều phải c/m

Ta có BĐT phụ \(\dfrac{1+\sqrt{a}}{1-a}\ge4a+1\)
\(\Leftrightarrow-\dfrac{\sqrt{a}\left(2\sqrt{a}-1\right)^2}{\sqrt{a}-1}\ge0\forall\dfrac{1}{4}< a< 0\)
Tương tự cho 3 BĐT còn lại ta cũng có:
\(\dfrac{1+\sqrt{b}}{1-b}\ge4b+1;\dfrac{1+\sqrt{c}}{1-c}\ge4c+1;\dfrac{1+\sqrt{d}}{1-d}\ge4d+1\)
Cộng theo vế 4 BĐT trên ta có:
\(VT\ge4\left(a+b+c+d\right)+4=8=VP\)
Xảy ra khi \(a=b=c=d=\dfrac{1}{4}\)
Ta cần chứng minh :
\(\dfrac{1+\sqrt{a}}{1-a}\ge4a+1\) \(\forall a\in\left(0;\dfrac{1}{4}\right)\)
\(\Leftrightarrow1+\sqrt{a}\ge\left(4a+1\right)\left(1-a\right)\)
\(\Leftrightarrow1+\sqrt{a}\ge4a-4a^2+1-a\)
\(\Leftrightarrow4a^2-4a-1+a+1+\sqrt{a}\ge0\)
\(\Leftrightarrow4a^2-3a+\sqrt{a}\ge0\)
\(\Leftrightarrow\left(4a^2-a\right)-\left(2a-\sqrt{a}\right)\ge0\)
\(\Leftrightarrow\left(2a-\sqrt{a}\right)\left(2a+\sqrt{a}\right)-\left(2a-\sqrt{a}\right)\ge0\)
\(\Leftrightarrow\left(2a-\sqrt{a}\right)\left(2a+\sqrt{a}-1\right)\ge0\)
Ta có: \(2a-\sqrt{a}=\left(\sqrt{2a}-\dfrac{\sqrt{2}}{4}\right)^2-\dfrac{1}{8}\ge0\) \(\forall a\in\left(0;\dfrac{1}{4}\right)\)
\(\left(2a+\sqrt{a}-1\right)=\left(\sqrt{2a}+\dfrac{\sqrt{2}}{4}\right)^2-\dfrac{9}{8}\ge0\)
\(\forall a\in\left(0;\dfrac{1}{4}\right)\)
Vậy: \(\dfrac{1+\sqrt{a}}{1-a}\ge4a+1\) \(\forall a\in\left(0;\dfrac{1}{4}\right)\)
Tương tự: \(\dfrac{1+\sqrt{b}}{1-b}\ge4b+1\forall b\in\left(0;1\right)\)
\(\dfrac{1+\sqrt{c}}{1-c}\ge4c+1\forall c\in\left(0;\dfrac{1}{4}\right)\)
\(\dfrac{1+\sqrt{d}}{1-d}\ge4d+1\forall d\in\left(0;\dfrac{1}{4}\right)\)
Cộng các BĐT vừa chứng minh, ta được:
\(\dfrac{1+\sqrt{a}}{1-a}+\dfrac{1+\sqrt{b}}{1-b}+\dfrac{1+\sqrt{c}}{1-c}+\dfrac{1+\sqrt{d}}{1-d}\ge4\left(a+b+c+d\right)+4=8\)
Vậy: Ta suy ra được điều phải chứng minh

\(\Leftrightarrow\dfrac{a}{\sqrt{4b^2+bc+4c^2}}+\dfrac{b}{\sqrt{4c^2+ca+4a^2}}+\dfrac{c}{\sqrt{4a^2+ab+4b^2}}\ge1\)
Ta có:
\(\sum\left(\dfrac{a}{\sqrt{4b^2+bc+4c^2}}\right)^2\sum a\left(4b^2+bc+4c^2\right)\ge\left(a+b+c\right)^3\)
Nên ta chỉ cần chứng minh:
\(\dfrac{\left(a+b+c\right)^3}{a\left(4b^2+bc+4c^2\right)+b\left(4c^2+ac+4a^2\right)+c\left(4a^2+ab+4b^2\right)}\ge1\)
\(\Leftrightarrow\dfrac{\left(a+b+c\right)^3}{4a\left(b^2+c^2\right)+4b\left(c^2+a^2\right)+4c\left(a^2+b^2\right)+3abc}\ge1\)
\(\Leftrightarrow a^3+b^3+c^3+3abc\ge ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\) (đúng theo Schur bậc 3)
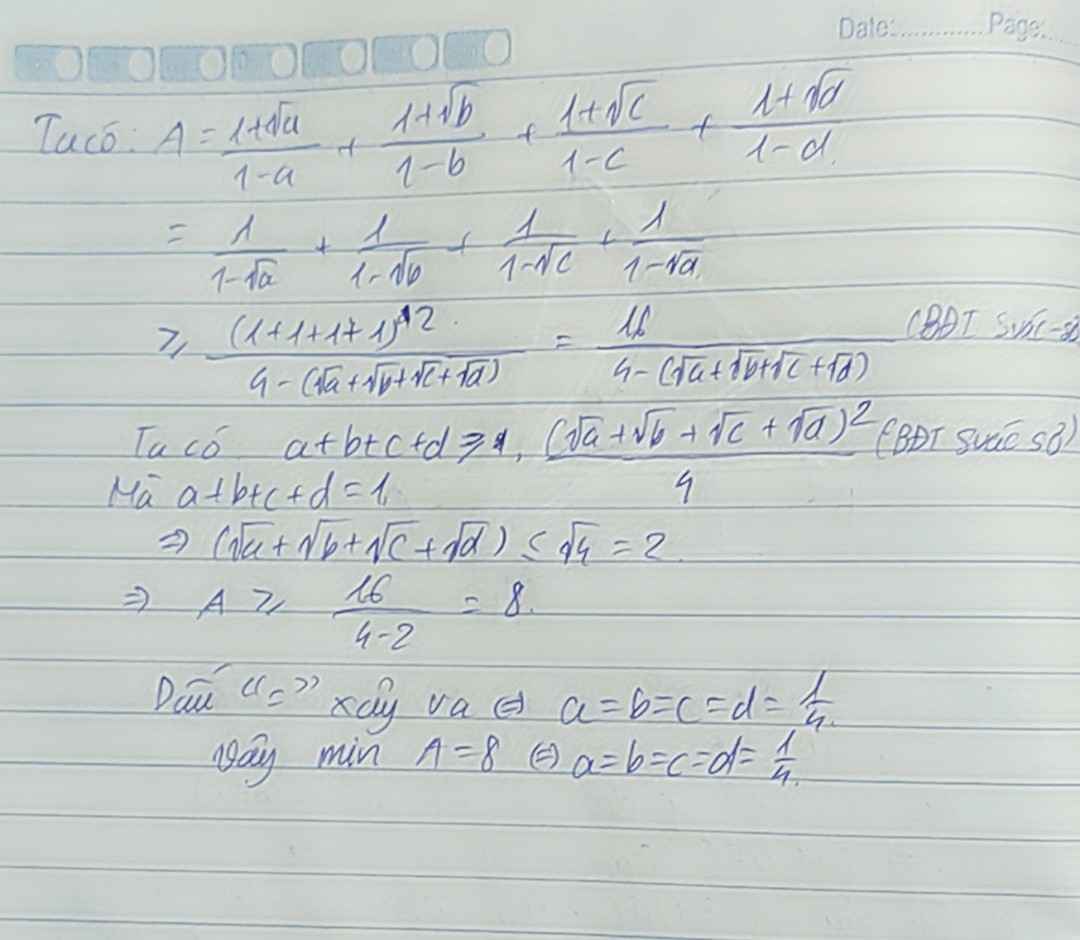
Lời giải:
Áp dụng BĐT AM-GM dạng ngược dấu (\(ab\leq (\frac{a+b}{2})^2\) )ta có:
\(\frac{b+c+d}{a}.1\leq \left(\frac{\frac{b+c+d}{a}+1}{2}\right)^2=\frac{(a+b+c+d)^2}{4a^2}\)
\(\Rightarrow \frac{a}{b+c+d}\geq \frac{4a^2}{(a+b+c+d)^2}\)\(\Rightarrow \sqrt{\frac{a}{b+c+d}}\geq \frac{2a}{a+b+c+d}\)
Hoàn toàn tương tự:
\(\left\{\begin{matrix} \sqrt{\frac{b}{c+d+a}}\geq \frac{2b}{a+b+c+d}\\ \sqrt{\frac{c}{d+a+b}}\geq \frac{2c}{a+b+c+d}\\ \sqrt{\frac{d}{a+b+c}}\geq \frac{2d}{a+b+c+d}\end{matrix}\right.\)
Cộng theo vế: \(\Rightarrow \text{VT}\geq \frac{2a+2b+2c+2d}{a+b+c+d}=2\)
Dấu bằng xảy ra khi \(\frac{b+c+d}{a}=\frac{c+d+a}{b}=\frac{d+a+b}{c}=\frac{a+b+c}{d}=1\)
\(\Leftrightarrow a+b+c+d=0\) (VL do $a,b,c,d$ dương)
Do đó dấu bằng không xảy ra .
Hay \(\text{VT}>2\) (đpcm)