Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có:
$y=xq$
$z=yq=xq^2$
Và:
$2y=x+d$
$3z=2y+d=x+2d$
$\Rightarrow 2xq=x+d$ và $3xq^2=x+2d$
$\Rightarrow 3xq^2-2xq=d$
$\Leftrightarrow xq(3q-2)=d$
Khi đó, thay vô $2xq=x+d$ thì:
$\frac{2d}{3q-2}=\frac{d}{q(3q-2)}+d$
$\Leftrightarrow \frac{2}{3q-2}=\frac{1}{q(3q-2)}+1$ (do $d\neq 0$)
$\Leftrightarrow 2q=1+q(3q-2)$
$\Leftrightarrow 3q^2-4q+1=0$
$\Leftrightarrow (q-1)(3q-1)=0$
Vì $q\neq 1$ nên $q=\frac{1}{3}$

Chọn A
Theo giả thiết ta có :
y = x q ; z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .
Nếu x = 0 ⇒ y = z = 0 ⇒ công sai của cấp số cộng: x ; 2y ; 3z bằng 0 (vô lí).
nếu
3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3 q = 1 .

Lời giải:
Có:
$b=a+d$
$c=a+2d$
$c=bq$
$a=bq^2$
$\Rightarrow abc=bq^2.b.bq=(bq)^3=8$
$\Rightarrow bq=2$
$\Rightarrow c=2$
$a=bq^2=bq.q=2q$
$b=a+d=2q+d$
$2=c=a+2d=2q+2d\Rightarrow q+d=1$
$\Rightarrow b=2q+d=q+(q+d)=q+1$. Mà $bq=2$ nên:
$q(q+1)=2$
$\Leftrightarrow (q-1)(q+2)=0$
$\Rightarrow q=1$ hoặc $q=-2$
Vì $a,b,c$ đều dương nên $q>0$. Do đó $q=1$

Ta có hệ phương trình:
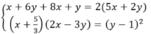
Từ đó ta suy ra
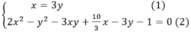
Thế (1) vào (2) ta được: 8y2+7y-1=0⇒y=-1 hoặc y=1/8
Do y < 0 , ta được y = -1, x = -3
Đáp án B

Chọn A
+ Ba số x + 6 y ,5 x + 2 y ,8 x + y lập thành cấp số cộng nên
x + 6 y + 8 x + y = 2 5 x + 2 y ⇔ 9 x + 7 y = 10 x + 4 y ⇔ x = 3 y
+ Ba số x + 5 3 , y − 1,2 x − 3 y lập thành cấp số nhân nên x + 5 3 2 x − 3 y = y − 1 2 .
Thay x= 3y vào ta được :
3 y + 5 3 2.3 y − 3 y = y − 1 2 ⇔ 3 y + 5 3 .3 y = y 2 − 2 y + 1 ⇔ 9 y 2 + 5 y − y 2 + 2 y − 1 = 0
⇔ 8 y 2 + 7 y − 1 = 0 ⇔ y = − 1 hoặc y = 1 8 .
Với y= -1 thì x= - 3; với y = 1 8 thì x = 3 8 .
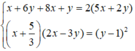
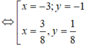
\(y=\dfrac{x+z}{2}\)
\(\left(y-4\right)^2=xz\)
\(\left(y-4\right)=\dfrac{x+z-9}{2}\)
3 pt 3 ẩn, kiên trì chút chắc giải được á :D