Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số mol Cu, Al,Mg lần lượt là x,y,z
\(\left\{{}\begin{matrix}64x+27y+24z=8,3\\1,5y+z=\dfrac{5,6}{22,4}\\x=\dfrac{1,12}{22,4}\end{matrix}\right.\)=>\(\left\{{}\begin{matrix}x=0,05\\y=0,1\\z=0,1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\%nCu=20\%\\\%nAl=40\%\\\%nMg=40\%\end{matrix}\right.\)
gọi số mol Cu, Al,Mg lần lượt là x,y,z
⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩64x+27y+24z=8,31,5y+z=5,622,4x=1,1222,4{64x+27y+24z=8,31,5y+z=5,622,4x=1,1222,4=>⎧⎪⎨⎪⎩x=0,05y=0,1z=0,1{x=0,05y=0,1z=0,1
=>⎧⎪⎨⎪⎩%nCu=20%%nAl=40%%nMg=40%

em ơi!
khi cho hỗn hợp Cu và Mg vào H2SO4 chỉ có Mg phản ứng, chất rắn còn lại là đồng
pt Mg + H2SO4 ===> MgSO4 + H2
(phản ứng) 0,25(mol) <==== \(\frac{5,6}{22,4}\)=0,25( mol)
+ cho B + H2SO4 đn:( vì H2SO4) vừa đủ nên chất rắn B có thể có cả Mg.
Mg0=> Mg 2+ + 2e Cu0====> Cu2+ + 2e
x======> 2x (mol) y=====> 2y
S6+ + 2e=====> S4+( S02)
0,1 <==== 0,05
BT electron có.
hpt...\(\begin{cases}2x+2y=0,1\\24x+64y=8,3-24.0.25=2,3\end{cases}\)====> \(\begin{cases}x=0,0225\\y=0,0275\end{cases}\)(mol)
===> tổng số mol hỗn hợp=0,05
=>\(\begin{cases}\%nMg=45\%\\\%nCu=55\%\end{cases}\)
ý b đầu bài nên chặt chẽ hơn! dd B. chất rắn còn lại cũng B vậy là sao?

Đáp án C.
Kim loại không phản ứng với H2SO4 loãng là Cu.
Gọi nCu = x, nMg = y, nAl = z
Ta có:
64x + 24y + 27z = 33,2 (1)
Bảo toàn e:
2nMg + 3nAl = 2nH2
=> 2y + 3z = 2.1 (2)
2nCu = 2nSO2 => x = 0.2 (mol) (3)
Từ 1, 2, 3 => x = 0,2; y = z = 0,4 (mol)
mCu = 0,2.64 = 12,8 (g)
mMg = 0,4.24 = 9,6 (g)
mAl = 10,8 (g)
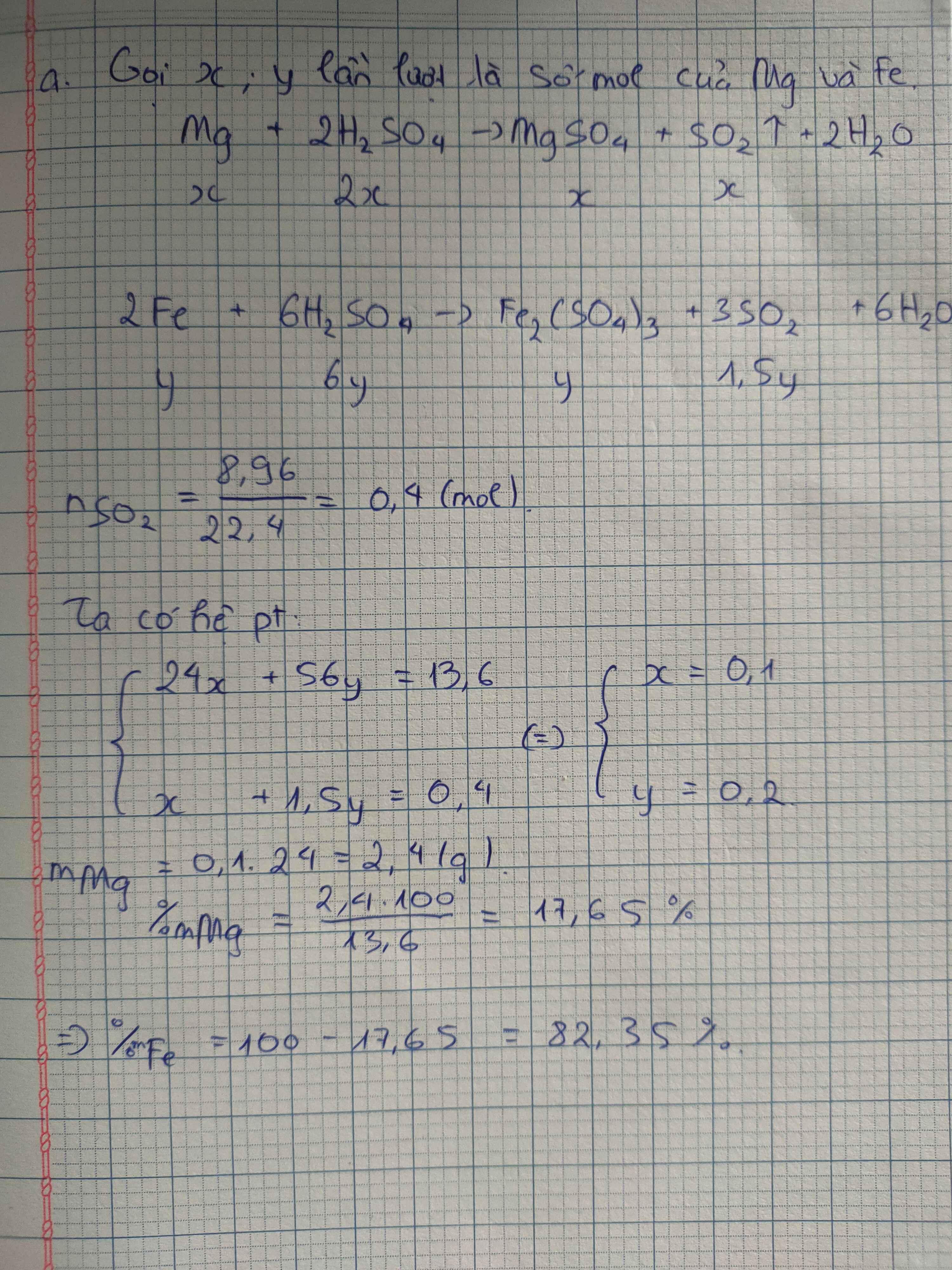

\(n_{H_2}=\dfrac{6,72}{22,4}=0,3\left(mol\right)\\ n_{SO_2}=\dfrac{2,24}{22,4}=0,1\left(mol\right)\)
PTHH:
2Al + 3H2SO4 ---> Al2(SO4)3 + 3H2
0,2<-----0,3<-----------0,1-------------0,3
Cu + 2H2SO4 ---> CuSO4 + SO2 + 2H2O
0,1<---------------------------------0,1
\(\rightarrow\left\{{}\begin{matrix}m_{Al}=0,2.27=5,4\left(g\right)\\m_{Cu}=0,1.64=6,4\left(g\right)\end{matrix}\right.\\ \rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{5,4}{11,8}.100\%=45,76\%\\\%m_{Cu}=100\%-45,76\%=54,24\%\end{matrix}\right.\)
\(m_{ddA}=\dfrac{0,3.98}{20\%}+5,4-0,3.2=151,8\left(g\right)\\ C\%_{Al_2\left(SO_4\right)_3}=\dfrac{0,1.342}{151,8}.100\%=22,53\%\)
tk: