Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

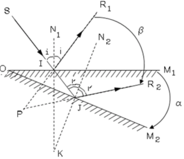
* Xét gương quay quanh trục O từ vị trí M1 đến vị trí M2 (Góc M1O M1 = a) lúc đó pháp tuyến cũng quay 1 góc N1KN2 = a (Góc có cạnh tương ứng vuông góc).
* Xét DIPJ có:
Góc IJR2 = ∠ J I P + ∠ I P J hay:
2i’ = 2i + b Þ b = 2(i’-i) (1)
* Xét DIJK có
∠ I J N 2 = ∠ J I K + ∠ I K J hay
i’ = i + a Þ a = 2(i’-i) (2)
Từ (1) và (2) ta suy ra b = 2a
Tóm lại: Khi gương quay một góc a quanh một trục bất kì thì tia phản xạ sẽ quay đi một góc 2a theo chiều quay của gương
Bạn giỏi giải bài đó thiệt đó gặp mình nhìn muốn lé con mắt lun

Ta có :
\(R_1.R_2=R_1IT-R_2IT\)
Mà \(R_1IT\) = \(S_1IG_1+a\)
\(R_2IT=R_2IK-a\)
\(\Rightarrow R_2IT=S_1IG_1-a\) (định luật phản xạ)
Thay vào : \(R_1IR_2=S_1IG_1+a+S_1IG-a_1\)
\(\Rightarrow2a\)
Xét gương quay quanh trục O từ vị trí M1 đến M2: góc M1OM2 = alpha
ta có góc alpha = góc N1KN2( góc có cạnh tương ứng vuông góc)
Xét tam giác EKJ: có 2i + góc beta = 2i1 hay: góc beta = 2( i1 - i) (1)
Xét tam giác IKJ: góc IKJ + i = i1 hay: góc alpha =( i1 -i) (2)
từ (1) và (2) suy ra: góc beta = 2 lần góc alpha.
Gương quay góc alpha quanh một trục nằm trên mặt gương và vuông góc với tia tới thì tia phản xạ quay 1 góc bằng 2 anpha, theo chiều kim đồng hồ.