K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

28 tháng 8 2016
1.
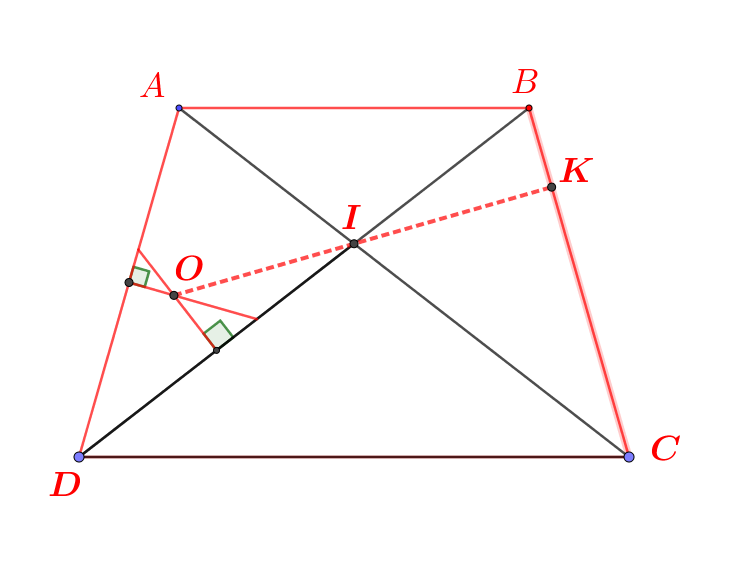
+) Tứ giác ABCD kà hình thang cân => góc ADC = BCD và AD = BC
=> tam giác ODC cân tại O => OD = OC
mà AD = BC => OA = OB
+) tam giác ODB và OCA có: OD = OC; góc DOC chung ; OB = OA
=> Tam giác ODB = OCA (c - g - c)
=> góc ODB = OCA mà góc ODC = OCD => góc ODC - ODB = OCD - OCA
=> góc EDC = ECD => tam giác EDC cân tại E => ED = EC (2)
Từ (1)(2) => OE là đường trung trực của CD
=> OE vuông góc CD mà CD // AB => OE vuông góc với AB
Tam giác OAB cân tại O có OE là đường cao nên đồng thời là đường trung trực
vậy OE là đường trung trực của AB


2)
Có: \(\left\{{}\begin{matrix}AB=AD\left(gt\right)\\AD=BC\left(2.cạnh.bên.hình.thang.cân\right)\end{matrix}\right.\)
\(\Rightarrow AB=BC\Rightarrow\Delta ABC.cân.tại.B\)
Mà AB // ED (gt)
\(\Rightarrow\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
=> CA là tia phân giác của góc C.