Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(100^2-99^2+98^2-97^2+...+2^2-1^2\)
\(=\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\)
\(=199+195+...+3\)
Số lượng số hạng:
\(\left(199-3\right):4+1=50\) (số hạng)
Tổng:
\(\left(3+199\right)\times50:2=5050\)
Lời giải:
$=(100^2-99^2)+(98^2-97^2)+....+(2^2-1^2)$
$=(100-99)(100+99)+(98-97)(98+97)+...+(2-1)(2+1)$
$=100+99+98+97+...+2+1=100(100+1):2=5050$

x2 + y2 +z2 + 2x - 4y+6z + 14=0
(x2 + 2x +1) + (y2 - 2.y.2 +22) + (z2 + 2.z.3 +32) =0
(x+1)2 + (y-2)2 +(z+3)2 =0
vì (x+1)2 >= 0; (y-2)2>=0 ; (z+3)2>=0
nên x+1=0 và y-2=0 và z+3=0
x=-1 ; y=2 ; z=-3
vậy x+y+z=-2

x2 + y2 + z2 + 2x - 4y + 6z = -14
=> x2 + y2 + z2 + 2x - 4y + 6z +14=0
=>(x2+2x+1)+(y2-4y+4)+(z2+6z+9)=0
=>(x+1)2+(y-2)2+(z+3)2=0
Ta thấy: \(\hept{\begin{cases}\left(x+1\right)^2\ge0\\\left(y-2\right)^2\ge0\\\left(z+3\right)^2\ge0\end{cases}}\)
=>(x+1)2+(y-2)2+(z+3)2\(\ge\)0
\(\Rightarrow\hept{\begin{cases}\left(x+1\right)^2=0\\\left(y-2\right)^2=0\\\left(z+3\right)^2=0\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-1\\y=2\\z=-3\end{cases}}\)
\(\Rightarrow x+y+z=\left(-1\right)+2+\left(-3\right)=-2\)
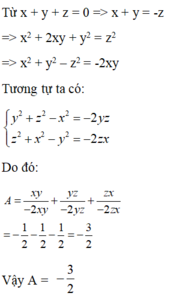
câu 6 bn chép thiếu
caau7: p = 10100/2
p = 2p - p = 5050